socp
语法
socp(f, [G], [h], [l], [q], [A], [b])
详情
该函数用于求解二阶锥规划问题,计算目标函数在限定条件下的最小值。若其约束条件以标准形式给出,其形式如下:
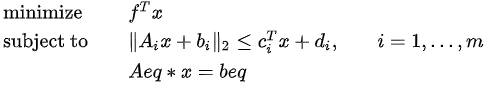
则矩阵 G 为:
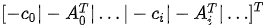
向量 h 为:
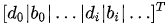
参数
二阶锥规划(Second-Order Cone Programming,SOCP)问题的约束条件形式如下:
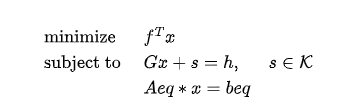
其中 K 为锥,s 为松弛变量,其值在优化过程中会被确定。
f 是数值型向量,表示目标函数的系数向量。
G 是数值型矩阵,表示锥约束的系数矩阵。
h 是数值型向量,表示锥约束的右端向量。
l 是整数标量,表示非负象限约束的维度。
q 是正数向量,表示各个二阶锥约束的维度大小,形式为 [r0,r1,…,rN-1]。
A 是数值型矩阵,表示等式约束的系数矩阵。
b 是数值型向量,表示等式约束的右端向量。
返回值
例子
求解以下二阶锥规划问题:
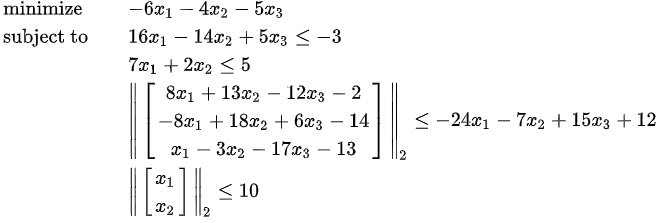
f = [-6, -4, -5]
G = matrix([[16, 7, 24, -8, 8, -1, 0, -1, 0],
[-14, 2, 7, -13, -18, 3, 0, 0, -1],
[5, 0, -15, 12, -6, 17, 0, 0, 0]])
h = [-3, 5, 12, -2, -14, -13, 10, 0, 0]
l = 2
q = [4,3]
re = socp(f,G,h,l,q, ,)
print(re)返回:("Optimal solution found",[-9.902804882871327,-1.39084684264198,26.211851780740154],-66.079042235904907)
