scs

语法

scs(f, [P], [A], [b], [Aeq], [beq], [lb], [ub], [x0], [c], [eps], [alpha])

详情

求解目标函数在约束条件下的最优解。具体模型如下：


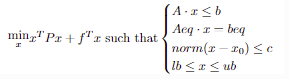
image

返回结果是具有两个元素的元组。第一个元素是目标函数的最小值，第二个元素是目标函数取最小值时，x 的取值。

参数

注：

以下参数中，除 lb, ub 可以为空外，其它参数都不可包含空值。

f 二次规划中的一次项系数向量。必须和 x0 长度相同。

P 一个矩阵，通过将二次项系数矩阵的对角线元素乘以2得到。例如：所有二次项组成上三角矩阵
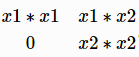
image
将对角线上的系数乘以2，其它系数不变，得到的矩阵就是 P。

A 线性不等式约束的系数矩阵。列数必须和 x 的长度相同。

b 线性不等式约束的右端向量。

Aeq 线性等式约束的系数矩阵。列数必须和 x 的长度相同。

beq 线性等式约束的右端向量。

lb 变量的下界。可以是标量或与 x 等长的向量。注意：当 lb 为空时，表示 x 无下界约束。

ub 变量的上界。可以是标量或与 x 等长的向量。注意：当 lb 为空时，表示 x 无上界约束。

若 lb 或 ub 是标量，则所有变量都受同一个下界或上界约束。若 lb 或 ub 为NULL，表示 x 无相应的下界或上界约束。

若 lb 或 ub 是向量，则 x 中的元素受 lb 或 ub 中相应位置的元素约束。若向量 lb 或 ub 中某元素为 NULL，表示此位置的 x 元素无相应的下界或上界约束

x0 向量绝对值不等式约束的系数向量。必须和 f 长度相同。

c 一个非负数字，表示绝对值不等式约束的右侧常量系数。

eps 正浮点数，表示求解的精度。默认值为1e-6，范围为 [1e-4, 1e-9]。通过减小该参数值以获得更高精度的解。如果该参数设置值超过规定范围，则会自动调整为默认值。

alpha 正浮点数，表示松弛参数。默认值为1.5，范围为 (0, 2)。通过增加 alpha 的值来加快求解速度。如果该参数设置值超过规定范围，则会自动调整为默认值。

例子

求 x, y 满足以下约束条件时，目标函数 x2 + y 2 的最小值


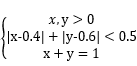
image
// 目标函数中没有一次项，所以系数都为0，f取值如下
f = [0, 0];
// 仅存在二次项x^2 和 y^2，系数为均为1，则 P 的取值为
P = [2, 0, 0, 2]$2:2;
// 绝对值不等式的约束系数和右端向量
x0 = [0.4, 0.6];
c = 0.5;
// 线性等式为 x+y=1，因此 Aeq 和 beq 的取值为
Aeq = [1, 1]$1:2;
beq = [1];
// 由 x,y>0 得到变量的下界
lb = [0, 0];
re = scs(f=f,P=P,Aeq=Aeq,beq=beq,lb=lb,x0=x0,c=c);
re[1]
// output
[0.500000043984074,0.499999955746447]

相关函数：linprog, quadprog