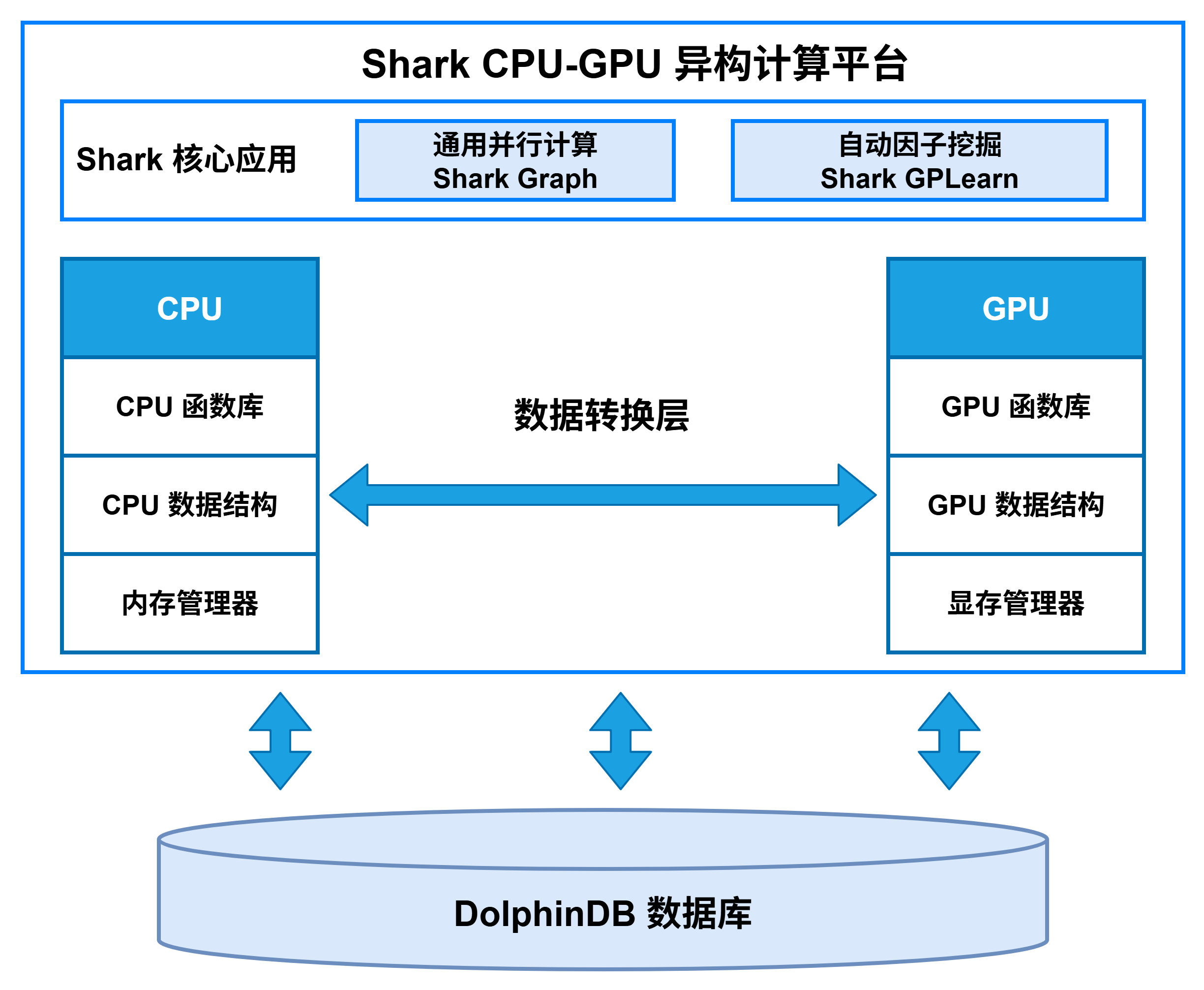
CPU-GPU 异构计算平台 Shark 应用:GPLearn 自动因子挖掘
因子挖掘是通过分析大量数据,识别影响资产价格变动的关键因素的过程。传统的因子挖掘方法主要基于经济理论与投资经验,难以有效表达复杂的非线性关系。随着数据集的丰富以及计算机算力的提升,基于遗传算法的自动因子挖掘方法已经被广泛应用。遗传算法通过随机生成公式,模拟自然界的进化过程,对于因子特征空间进行全面、系统的搜索,能够发现传统方法难以构建的隐藏因子。
1. Shark 介绍
Shark 是 DolphinDB 3.0 推出的 CPU-GPU 异构计算平台。它以 DolphinDB 的高效存储系统为底层支撑,深度融合 GPU 并行算力,能够为计算密集型任务提供显著的性能加速。Shark 平台基于 CPU-GPU 异构计算框架,提供两大核心功能:
-
Shark Graph:通过 GPU 加速 DolphinDB 的通用计算脚本,实现复杂分析任务的并行化执行。
-
Shark GPLearn:专为因子挖掘场景设计,支持基于遗传算法的自动化因子发现与优化。
通过这些功能,Shark 能够帮助 DolphinDB 突破 CPU 算力瓶颈,显著提升 DolphinDB 在高频量化、实时风控等大规模数据分析场景下的计算效率。
2. Shark GPLearn
2.1 功能介绍
Shark GPLearn 是基于 Shark 异构计算平台的高性能因子挖掘模块,可以直接从 DolphinDB 中读取数据,并调用 GPU 进行自动因子挖掘与因子计算,提高投研效率,适用于对性能具有较高要求的各类因子挖掘场景。
相较于 Python GPLearn ,Shark GPLearn 提供了更为丰富的算子库,包括使用三维数据的相关算子,并且提供了高效的 GPU 版本实现;Shark 引入了分组语义,支持在训练中进行分组计算;对于快照频、分钟频等中高频原始特征数据,Shark 也可以进行分钟频、日频的因子挖掘;同时为了充分发挥 GPU 的性能,Shark 支持单机多卡进行遗传算法因子挖掘。目前 Shark 支持的算子详见 Shark GPLearn 快速上手。
2.2 工作流程
Shark GPLearn 主要分为两大模块,GPLearnEngine 和 GPExecutor,基本架构如下图所示:
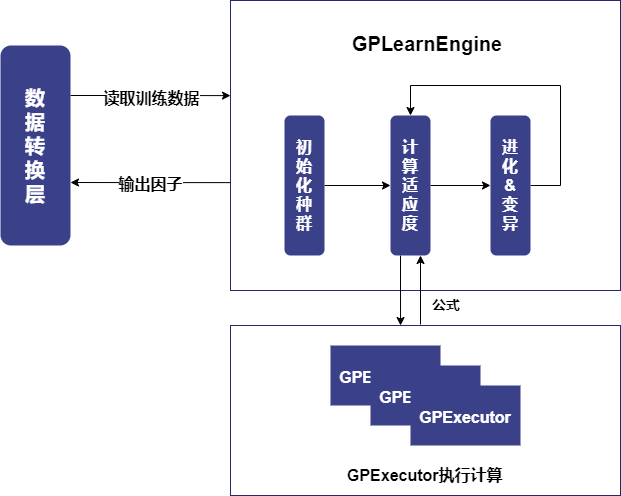
GPLearnEngine 主要负责训练时的调度工作,包括种群生成、进化和变异操作等。GPLearnEngine 在初始化阶段会生成初始公式种群,通过预先设定的目标函数,衡量这些公式与给定目标数据的相符程度。对于不同的应用,可以采用不同的适应度函数:例如回归问题可以采用目标值与公式结果间的均方误差,对于遗传算法生成的量化因子,可以使用因子 IC 作为适应度。
之后,GPLearnEngine 会从这些公式中,依据适应度选出合适的公式作为下一代进化的父代。这些被选择出来的公式会通过多种方式进行进化,包括交叉变异(Crossover Mutation)、子树变异(Subtree Mutation)、Hoist变异(Hoist Mutation)以及点变异(Point Mutation)的四种变异方式。
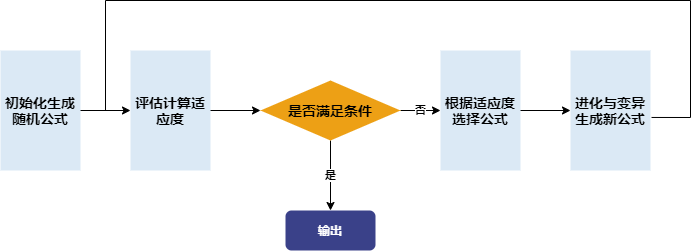
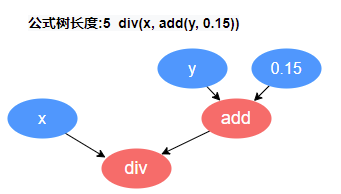
GPExecutor 主要负责对挖掘出的因子进行适应度计算。它首先将二叉树转化为后缀表达式(逆波兰表达式),举例来说,形如
div(x,add(y,0.15)) 的公式,会被转换为 [0.15, y, add, x,
div] 的形式。这个表达式的逆序就是因子的执行队列,队列中的变量与常量被称为数据算子,队列中的函数被称为函数算子。
之后,GPExecutor 会按照顺序遍历这个执行队列。对于数据算子,GPExecutor 会加载相应的数据入栈;而对于函数算子,则会依据函数的参数,将相应的参数出栈,然后利用 GPU 执行相应的函数,并将最终的结果入栈。最终,栈中的元素就是因子值,得到因子值后,GPExecutor 将会调用适应度函数与预测数据计算适应度。
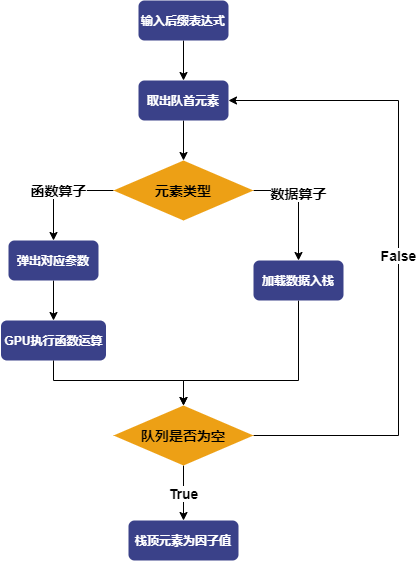
目前 Shark GPLearn 还支持降频因子挖掘的功能。在创建引擎时,可以通过参数指定聚合列。在进行模型训练时会根据聚合列进行分组,并随机选择聚合函数进行聚合计算。在降频因子挖掘的过程中,Shark 会通过函数签名,实现算子维度层面的约束,从而自动生成含有降频因子的因子表达式,并由 GPExecutor 实现表达式运算。
2.3 快速上手:符号回归
快速部署测试环境的方式请参考 Shark GPLearn 快速上手第 2 章。
符号回归是一种机器学习方法,无需假定函数的具体形式即可自动发现给定数据集的数学表达式或函数。符号回归的核心在于通过搜索算法,预先设定目标函数,在可能的数学表达式空间中找到最佳表达式,使其能够最大程度地拟合数据。符号回归的实现目前主要以遗传编程(Genetic Programming, GP)为主。
为了帮助初学者更好地上手 Shark GPLearn 进行因子挖掘,本文安排了一个符号回归的场景,假设目标函数为如下形式:
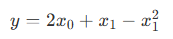
首先,模拟训练特征 trainData 和回归目标 targetData:
// 目标函数形式
def targetFunc(x0, x1){
return mul(x0,2)+x1-pow(x1,2)
}
// 模拟数据: 构造一个 x0∈[-1, 1], x1∈[-1, 1] 的网格坐标
x = round(-1 + 0..20*0.1, 1)
x0 = take(x, size(x)*size(x))
x1 = sort(x0)
trainData = table(x0, x1)
targetData = targetFunc(x0, x1)创建 Shark GPLearn 引擎,设置适应度函数、变异概率等相关参数,执行符号回归任务并返回适应度最优的数学表达式。
// 创建 GPLearnEngine 引擎
engine = createGPLearnEngine(
trainData, // 自变量
targetData, // 因变量
populationSize=1000, // 每代种群数量
generations=20, // 迭代次数
stoppingCriteria=0.01, // 表示提前终止迭代的适应度阈值
tournamentSize=20, // 锦标赛规模, 表示生成下一代公式时,参与竞争的公式数量
functionSet=["add", "sub", "mul", "div", "sqrt", "log", "reciprocal", "pow"], // 算子库
fitnessFunc="mse", // 适应度函数, 可选: ["mse","rmse","pearson","spearman","mae"]
initMethod="half", // 初始公式树生成规则
initDepth=[1, 4], // 初始化公式树深度范围
restrictDepth=true, // 是否严格限制公式长度
constRange=[0, 2.0], // 公式中包含的常量的范围, 为0时生成的公式将不包括常量
seed=123, // 随机种子
parsimonyCoefficient=0.01, // 公式复杂度的惩罚系数
crossoverMutationProb=0.8, // crossover的概率
subtreeMutationProb=0.1, // subtree的概率
hoistMutationProb=0.0, // hoist变异的概率
pointMutationProb=0.1, // point变异的概率
minimize=true, // 是否向适应度最小的方向进化
deviceId=0, // 指定使用的设备ID
verbose=true // 是否输出训练时的信息
)
// 获取适应度最优的公式
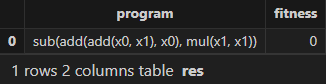
res = engine.gpFit(1) // Shark GPLearn的结果表
resShark GPLearn 返回的表达式以及适应度结果如下所示,可以发现 Shark GPLearn 完全拟合了目标函数:
3. 应用案例
3.1 日频因子挖掘
3.1.1 数据准备
首先,利用 DolphinDB 的 loadText 函数读取附件中的 DailyKBar.csv
日频行情数据集,并划分训练集与测试集。这里设置训练集的范围为 2020.08.12 至 2022.12.31 的所有交易日,测试集为
2023.01.01 至 2023.06.19 的所有交易日。
def processData(splitDay=2022.12.31){
// 数据源: 这里选择从 csv 读取, 需要用户根据实际情况修改文件路径
fileDir = "/home/fln/DolphinDB_V3.00.4/demoData/DailyKBar.csv"
colNames = ["SecurityID","TradeDate","ret20","preclose","open","close","high","low","volume","amount","vwap","marketvalue","turnover_rate","pctchg","PE","PB"]
colTypes = ["SYMBOL","DATE","DOUBLE","DOUBLE","DOUBLE","DOUBLE","DOUBLE","DOUBLE","INT","DOUBLE","DOUBLE","DOUBLE","DOUBLE","DOUBLE","DOUBLE","DOUBLE"]
t = loadText(fileDir, schema=table(colNames, colTypes))
// 获取训练特征: 训练特征需要 FLOAT / DOUBLE 类型; 且训练数据最好根据分组列进行排序
data =
select SecurityID, TradeDate as TradeTime,
preclose, // 昨收价
open, // 开盘价
close, // 收盘价
high, // 最高价
low, // 最低价
double(volume) as volume, // 成交量
amount, // 成交额
pctchg, // 涨跌幅
vwap, // 成交均价
marketvalue, // 总市值
turnover_rate, // 换手率
double(1\PE) as EP, // 盈利收益率
double(1\PB) as BP, // 账面市值比
ret20 // 未来20日收益率
from t order by SecurityID, TradeDate
// 划分训练集
days = distinct(data["TradeTime"])
trainDates = days[days<=splitDay]
trainData = select * from data where TradeTime in trainDates order by SecurityID, TradeTime
// 划分测试集
testDates = days[days>splitDay]
testData = select * from data where TradeTime in testDates order by SecurityID, TradeTime
return data, trainData, testData
}
splitDay = 2022.12.31 // 训练集和测试集的分割点
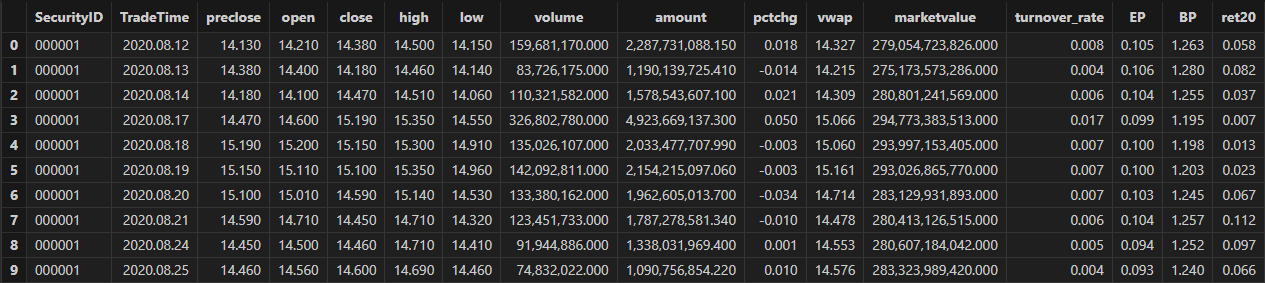
allData, trainData, testData = processData(splitDay) // 所有数据, 训练数据, 测试数据日频行情数据集的数据结构如下所示:
3.1.2 模型训练
创建 Shark GPLearnEngine。引擎提供丰富的参数可以供用户进行配置和调整。具体的参数含义和用法,可以参考文档:createGPLearnEngine。
在下面的例子中,对 functionSet、initProgram 等参数进行了配置。
-
functionSet,生成公式时使用的算子库。可以配置一些常用的滑动窗口函数。
-
initProgram,初始种群。支持用户自定义初始种群。
-
groupCol,分组列。使用滑动窗口函数时,支持分组计算。
-
minimize,是否最小化。支持用户指定进化的方向。
-
parsimonyCoefficient,惩罚系数。对公式长度可以进行限制。
trainX = dropColumns!(trainData.copy(), ["TradeTime", "ret20"]) // 训练数据自变量
trainY = trainData["ret20"] // 训练数据因变量
trainDate = trainData["TradeTime"] // 训练数据时间信息
// 配置算子库
functionSet = ["add", "sub", "mul", "div", "sqrt", "reciprocal", "mprod", "mavg", "msum", "mstdp", "mmin", "mmax", "mimin", "mimax","mcorr", "mrank", "mfirst"]
// 定义初始公式
alphaFactor = {
// world quant 101
"wqalpha6":<-1 * mcorr(open, volume, 10)>,
"wqalpha12":<signum(deltas(volume)) * (-1 * deltas(close))>,
"wqalpha26":<-1 * mmax(mcorr(mrank(volume, true, 5), mrank(high, true, 5), 5), 3)>,
"wqalpha35":<mrank(volume, true, 32) * (1 - mrank((close + high - low), true, 16)) * (1 - mrank((ratios(close) - 1), true, 32))>,
"wqalpha43":<mrank(div(volume, mavg(volume, 20)), true, 20) * mrank(-1*(close - mfirst(close, 8)), true, 8)>,
"wqalpha53":<-1 * (div(((close - low) - (high - close)), (close - low)) - mfirst(div(((close - low) - (high - close)), (close - low)), 10))>,
"wqalpha54":<-1 * div((low - close) * pow(open, 5), (low - high) * pow(close, 5))>,
"wqalpha101":<div(close - open, high - low + 0.001)>,
// 国泰君安 191
"gtjaAlpha2":<-1 * deltas(div(((close - low) - (high - close)), (high - low)))>,
"gtjaAlpha5":<-1 * mmax(mcorr(mrank(volume, true, 5), mrank(high, true, 5), 5), 3)>,
"gtjaAlpha11":<msum(div((close - low - (high - close)),(high - low)) * volume, 6)>,
"gtjaAlpha14":<close - mfirst(close, 6)>,
"gtjaAlpha15":<deltas(open) - 1>,
"gtjaAlpha18":<div(close, mfirst(close, 6))>,
"gtjaAlpha20":<div(close - mfirst(close, 7), mfirst(close, 7)) * 100>
}
initProgram = take(alphaFactor.values(), 600) // 初始种群
// 创建 GPLearnEngine 引擎
engine = createGPLearnEngine(trainX,trainY, // 训练数据
groupCol="SecurityID", // 分组列: 按 SecurityID 分组滑动
seed=42, // 随机数种子
populationSize=1000, // 种群规模
generations=10, // 进化次数
tournamentSize=20, // 锦标赛规模, 表示生成下一代公式时,参与竞争的公式数量
functionSet=functionSet, // 算子库
initProgram=initProgram, // 初始种群
minimize=false, // false表示最大化适应度
initMethod="half", // 初始化方法
initDepth=[2, 4], // 初始公式树种群深度
restrictDepth=true, // 是否严格限制树的深度
windowRange=[5,10,20,40,60], // 窗口大小范围
constRange=0, // 0表示公式禁止额外生成常量
parsimonyCoefficient=0.05,// 复杂度惩罚系数
crossoverMutationProb=0.6,// crossover的概率
subtreeMutationProb=0.01, // subtree的概率
hoistMutationProb=0.01, // hoist变异的概率
pointMutationProb=0.01, // point变异的概率
deviceId=0 // 指定使用的设备ID
)其中参数 parsimonyCoefficient 为节俭系数,用于限制公式树的长度,其作用是在适应度计算时,按照以下方式计算惩罚后的适应度作为新的适应度:
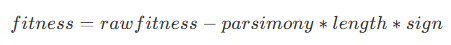
其中,rawfitness 表示原始适应度,parsimony 即为节俭系数,length 表示公式树长度,sign 表示适应度进化方向,当适应度进化方向为正时,其值为 1,反之为 -1。在 Shark 中:
-
当最小化适应度作为目标时,节俭系数为正表示鼓励更短的公式树,节俭系数为负表示鼓励更长的公式树
-
当最大化适应度作为目标时,节俭系数为正表示鼓励更长的公式树,节俭系数为负表示鼓励更短的公式树
在因子挖掘场景中,基于因子的金融属性,我们可以将 rankIC 设置为模型的适应度函数,指导模型挖掘和收益率相关性更高的因子公式。即我们需要将模型的适应度函数设置为:训练产生的因子值分日期计算 RankIC 后的均值,使用公式如下:
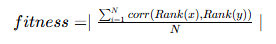
其中,N 为分组数量,这里就是训练集中包含的交易日数量。调用 setGpFitnessFunc
将自定义适应度函数以及用到的日期分组列传入 GPLearnEngine。目前 DolphinDB 支持在自定义适应度函数中添加
groupby、contextby、rank、zscore 等辅助算子,完整辅助算子详见 setGpFitnessFunc
函数页面。
// 修改适应度函数为自定义函数: 计算 rank IC
def myFitness(x, y, groupCol){
return abs(mean(groupby(spearmanr, [x, y], groupCol)))
}
setGpFitnessFunc(engine, myFitness, trainDate)模型配置完成后,即可调用 gpFit 函数进行模型训练,并返回适应度前 programNum 的因子公式。
// 训练模型,挖掘因子
programNum=30
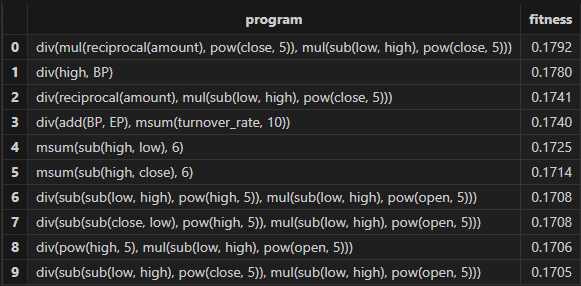
timer res = engine.gpFit(programNum)
// 查看挖掘结果
resShark GPLearn 返回适应度较优的因子结果表如下所示:
3.1.3 因子评价
模型训练完成后,可以用 gpPredict 函数进行因子计算。
allX = dropColumns!(allData.copy(), ["TradeTime", "ret20"]) // 所有数据自变量
// 计算所有因子值
factorValues = gpPredict(engine, allX, programNum=programNum, groupCol="SecurityID")
factorList = factorValues.colNames() // 因子列表
totalData = table(allData, factorValues)本文借助了 DolphinDB 的 alphalens 模块(Alphalens 在 DolphinDB 中的应用:因子分析建模实践)进行单因子评价函数的开发。
本教程中的单因子评价函数在原有基础上进行了如下处理:
-
数据预处理:
-
对因子值首先采用了 zscore 标准化处理。
-
调用 alphalens 的
get_clean_factor_and_forward_returns函数, 计算其未来不同周期的收益率,并对每天的因子值按分位数分组
-
-
IC 法:
-
调用 alphalens 的
factor_information_coefficient函数,计算因子每天的 rankIC。
-
-
分层回测:
-
按照持仓周期手动调整因子分组。比如持仓周期为5,则持仓周期的后4天因子分组沿用第一天的分组情况。
-
调用 alphalens 的
mean_return_by_quantile函数,计算每个组在未来不同周期的平均收益率。 -
调用 alphalens 的
plot_cumulative_returns_by_quantile函数将平均收益转换为累积收益,从而直观对比不同分位数组合的长期表现和分化情况。
-
具体代码如下:
/*
自定义单因子评价函数
@params:
totalData: 因子数据
factorName: 因子名称, 用于从 totalData 里查询指定因子值
priceData: 价格数据, 用于计算因子收益率
returnIntervals: 持仓周期列表
quantiles: 分位数分档, 用于因子分层
*/
def singleFactorAnalysis(totalData, factorName, priceData, returnIntervals, quantiles){
print("factorName: "+factorName+" analysis start")
/* 数据预处理, 计算未来不同周期收益和每期的因子分组 */
// 取出单因子值, 并进行标准化处理
factorVal = eval(<select TradeTime as date, SecurityID as asset, zscore(_$factorName) as factor from totalData context by TradeTime>)
// 调用 alphalens 的 get_clean_factor_and_forward_returns 函数, 计算其未来不同周期的收益率,并进行因子值分组,生成中间分析结果。
periods = distinct(returnIntervals<-[1]).sort()
cleanFactorAndForwardReturns = alphalens::get_clean_factor_and_forward_returns(
factor=factorVal, // 因子数据
prices=priceData, // 价格数据
quantiles=quantiles, // 分位数分档
periods=periods, // 未来收益周期
max_loss=0.1, // 最大数据丢弃容忍度。数据清洗过程中可能会丢弃一些无效数据(如因子为NaN,或计算不出收益)。
// 此参数设置一个比例(如0.1代表10%),如果丢弃的数据超过这个比例,函数会报错。设为0表示不允许丢弃任何数据。
cumulative_returns=true // 多期收益是否累计收益
)
/* IC法做因子评价 */
// 调用 alphalens 的 factor_information_coefficient 函数, 计算因子每天的rankIC
factorRankIC = select factorName as `factor, * from alphalens::factor_information_coefficient(cleanFactorAndForwardReturns)
factorRankIC = select factor, date, int(each(last, valueType.split("_"))) as returnInterval, value as rankIC
from unpivot(factorRankIC, keyColNames=`factor`date, valueColNames=factorRankIC.colNames()[2:])
/* 分层回测法做因子评价 */
// 获取所有回测时间点
timeList = sort(distinct(totalData["TradeTime"]))
// 获取用于分层回测的数据
sliceData = select date, asset, forward_returns_1D, factor_quantile, factor_quantile as periodGroup from cleanFactorAndForwardReturns
// 构造针对每个持仓周期进行分组回测的处理函数
quantileTestFun = def(timeList, sliceData, returnInterval){
// 根据持仓周期给每个回测时间划分持仓周期分组
periodDict = dict(timeList, til(size(timeList))/returnInterval)
// 根据持仓周期分组, 替换周期内的分组信息。(比如持仓周期为5, 则后四天因子分组沿用第一天的分组情况)
update sliceData set factor_quantile = periodGroup[0] context by asset, periodDict[date]
tmp = select * from sliceData where factor_quantile!=NULL
ret, stdDaily = alphalens::mean_return_by_quantile(sliceData, by_date=true, demeaned=false)
ret = alphalens::plot_cumulative_returns_by_quantile(ret, period="forward_returns_1D")
// 调整结果表
groupCols = sort(ret.colNames()[1:])
res = eval(<select date as `TradeTime, returnInterval as `returnInterval, _$$groupCols as _$$groupCols from ret order by date>)
return res
}
// 计算不同持仓周期的分层回测结果
quantileRes = select factorName as `factor, * from each(quantileTestFun{timeList, sliceData}, returnIntervals).unionAll()
print("factorName:"+factorName+"analysis finished")
return factorRankIC, quantileRes
}将开发的自定义单因子评价函数,通过 peach 函数批量应用于 shark GPLearnEngine
挖掘出来的每一个因子。最终可生成以下因子评价结果:
-
rankICRes:在不同未来收益区间下,各因子的 RankIC 序列;
-
quantileRes:按因子值分组后,各时间点对应的区间收益率表现;
-
rankICStats:在训练集、测试集及全量数据上的统计指标,包括 RankIC 均值、RankIC IR,以及 RankIC 序列中与 RankIC 均值方向一致的比例。
/*
因子批量回测
@params:
totalData: 因子数据
factorName: 因子列表
returnIntervals: 持仓周期列表
quantiles: 分位数分档
splitDay: 训练集和测试集的日期分界线
*/
def analysisFactors(totalData, factorList, returnIntervals, quantiles=5, splitDay=2022.12.31){
// 获取每个时间点对应的价格数据
priceData = select close from totalData pivot by TradeTime as date, SecurityID
// 单因子评价
resDataList = peach(singleFactorAnalysis{totalData, , priceData, returnIntervals, quantiles}, factorList)
// 结果汇总
rankICRes = unionAll(resDataList[, 0], false)
quantileRes = unionAll(resDataList[, 1], false)
// 对所有数据的 rankIC 结果进行分析
calICRate = defg(rankIC){return sum(signum(avg(rankIC))*rankIC > 0) \ count(rankIC)}
allRankIC = select avg(rankIC) as rankIC,
avg(rankIC) \ stdp(rankIC) as rankICIR,
calICRate(rankIC) as signRate
from rankICRes group by factor, returnInterval
// 对训练集数据的 rankIC 结果进行分析
trainRankIC = select avg(rankIC) as trainRankIC,
avg(rankIC) \ stdp(rankIC) as trainRankICIR,
calICRate(rankIC) as trainSignRate
from rankICRes where date<=splitDay group by factor, returnInterval
// 对测试集数据的 rankIC 结果进行分析
testRankIC = select avg(rankIC) as testRankIC,
avg(rankIC) \ stdp(rankIC) as testRankICIR,
calICRate(rankIC) as testSignRate
from rankICRes where date>splitDay group by factor, returnInterval
// 结果汇总
factor = table(factorList as factor)
rankICStats = lj(factor, lj(allRankIC, lj(trainRankIC, testRankIC, `factor`returnInterval), `factor`returnInterval), `factor)
return rankICRes, quantileRes, rankICStats
}
/* 单因子分析
rankICRes: 查看因子 rankIC 明细表
quantileRes: 查看分层收益率最终结果表
rankICStats: 查看 rankIC 分析表
*/
rankICRes, quantileRes, rankICStats = analysisFactors(totalData, factorList, returnIntervals=[1,5,10,20,30], quantiles=[0.0, 0.2, 0.4, 0.6, 0.8, 1.0], splitDay=splitDay)
3.1.4 结果可视化
在本示例中,我们基于 RankIC 均值、RankICIR 绝对值以及 IC 胜率三个指标对因子进行筛选。具体筛选条件为:RankIC 均值绝对值不低于 0.05、RankICIR 绝对值不低于 0.5,且 IC 胜率超过 65%。运行以下代码可得到最终筛选出的日频优选因子。读者可根据实际策略需求灵活调整筛选规则。
// 因子筛选
retInterval = 20 // 选取展示的持仓周期
factorPool =
select * from rankICStats
where returnInterval=retInterval
and abs(rankIC)>=0.05 and abs(rankICIR)>=0.5 and signRate>=0.65
and isDuplicated([round(abs(rankIC), 4), round(abs(rankICIR), 4)])=false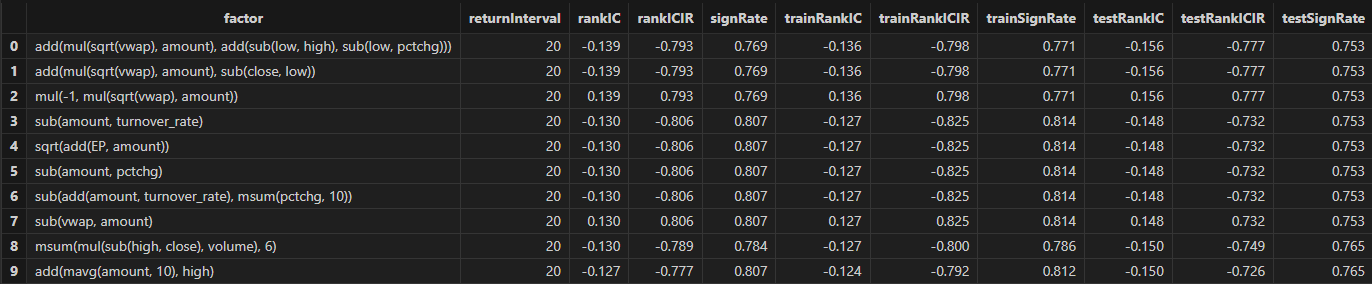
运行以下代码查看 Shark GPLearn 返回的日频优选因子的日频 RankIC 与累计 RankIC 结果:
// 日频 RankIC 与累计 RankIC 可视化
factorName = factorPool[`factor][0] // 选取展示的因子
sliceData = select date, rankIC, cumsum(RankIC) as cumRankIC from rankICRes where factor=factorName and returnInterval=retInterval
plot(sliceData[`rankIC`cumRankIC], sliceData[`date], extras={multiYAxes: true})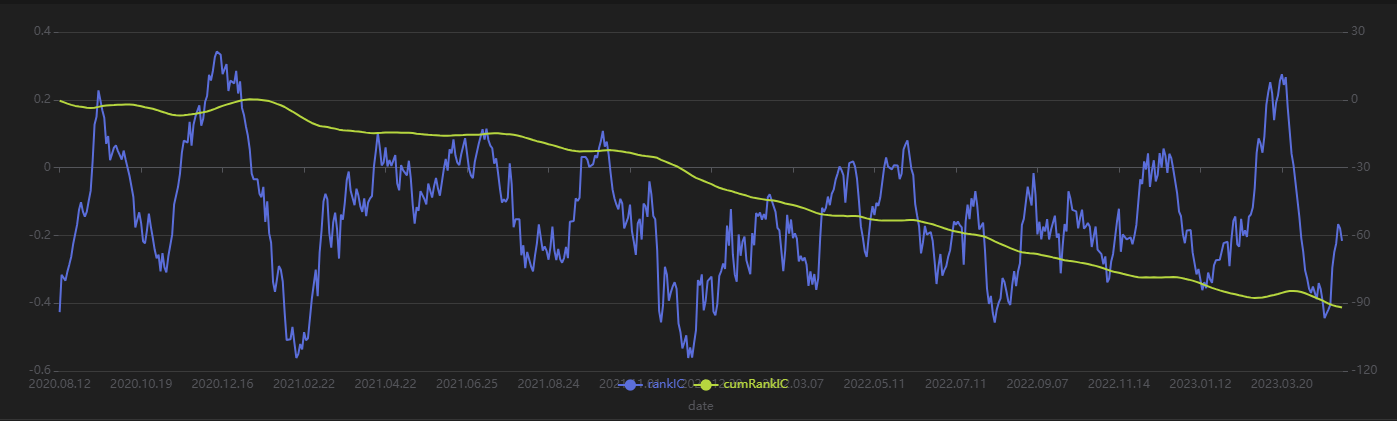
从上图可以看出,该因子的 RankIC 表现无论在训练期(2023 年以前)还是测试期(2023 年以后)都较为稳定:大部分时间该因子的 RankIC 均处于 0 值以下,RankIC 累计值直线向下。
运行以下代码查看 Shark GPLearn 返回的日频优选因子的不同日频区间收益率下的 RankIC 结果,可以发现,该因子对于未来 1~30 日收益率均有较好的预测能力:
// rankIC 均值可视化
sliceData = select * from rankICStats where factor=factorName
plot(sliceData[`rankIC`trainRankIC`testRankIC], sliceData[`returnInterval])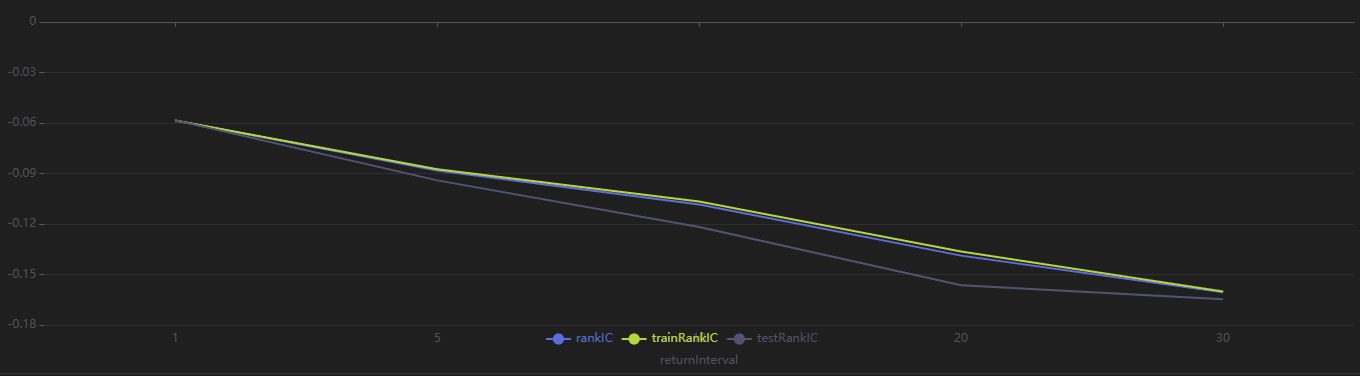
运行以下代码查看每 20 个交易日按第一天的因子值分组回测得到的分层收益率。从下图可以发现分层回测的整体结果与 IC 法的结果一致——该因子利用未来 20 日区间收益率计算的 IC 值显著为负。使用 20 日调仓周期分层回测发现:因子值最高的分组(分组 5) 整体收益最低,因子值最低的分组(分组 1)整体收益最高,组间分层明显,说明该因子表现优良。
// 分层收益率可视化
sliceData = select * from quantileRes where factor=factorName and returnInterval=retInterval
plot(sliceData[columnNames(sliceData)[3:]],sliceData[`TradeTime]) 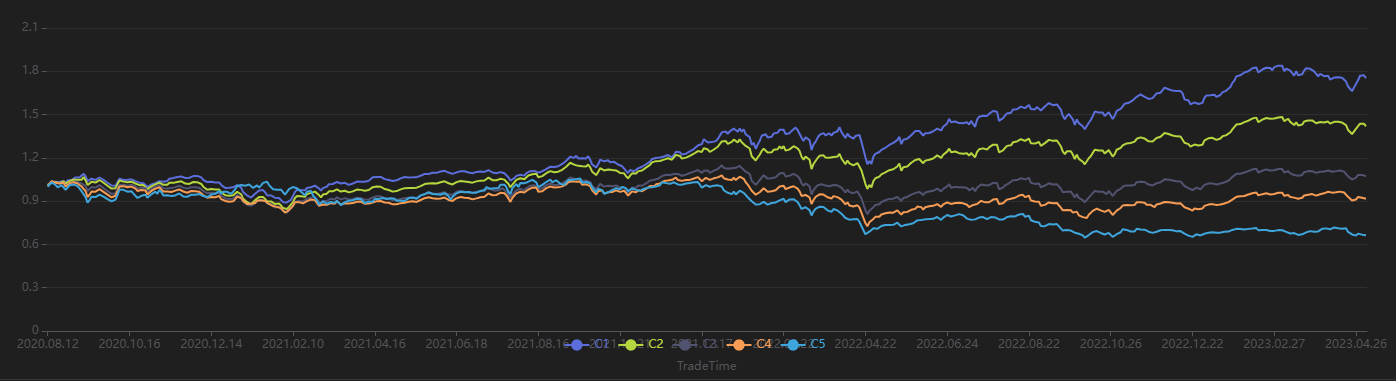
3.2 分钟频因子挖掘
3.2.1 数据准备
首先,利用 DolphinDB 的 loadText 函数读取附件中的 MinuteKBar.csv
日频行情数据集,并划分训练集与测试集。这里设定训练集范围为 2021-03-01 至 2021-10-31 期间的交易日,测试集范围为
2021-11-01 至 2021-12-31 期间的交易日。
def processData(splitDay=2021.11.01){
// 数据源: 这里选择从 csv 读取, 需要用户根据实际情况修改文件路径
fileDir = "/home/fln/DolphinDB_V3.00.4/demoData/MinuteKBar.csv"
colNames = ["SecurityID","TradeTime","preclose","open","high","low","close","volume","amount"]
colTypes = ["SYMBOL","TIMESTAMP","DOUBLE","DOUBLE","DOUBLE","DOUBLE","DOUBLE","INT","DOUBLE"]
t = loadText(fileDir, schema=table(colNames, colTypes))
// 获取训练特征: 训练特征需要 FLOAT / DOUBLE 类型; 且训练数据最好根据分组列进行排序
data =
select SecurityID,
TradeTime, // 时间列
preclose, // 昨收价
open, // 开盘价
close, // 收盘价
high, // 最高价
low, // 最低价
double(volume) as volume, // 成交量
amount, // 成交额
nullFill(ffill(Amount \ Volume), 0.0) as vwap,// 成交均价
move(close,-241)\close-1 as ret240 // 未来240分钟收益率
from t context by SecurityID order by SecurityID, TradeTime
data = select * from data where not isNull(ret240)
// 划分训练集
days = distinct(data["TradeTime"])
trainDates = days[days<=splitDay]
trainData = select * from data where TradeTime in trainDates order by SecurityID, TradeTime
// 划分测试集
testDates = days[days>splitDay]
testData = select * from data where TradeTime in testDates order by SecurityID, TradeTime
return data, trainData, testData
}
splitDay = 2021.11.01 // 训练集和测试集的分割点
allData, trainData, testData = processData(splitDay) // 所有数据, 训练数据, 测试数据分钟频行情数据集的数据结构如下所示:
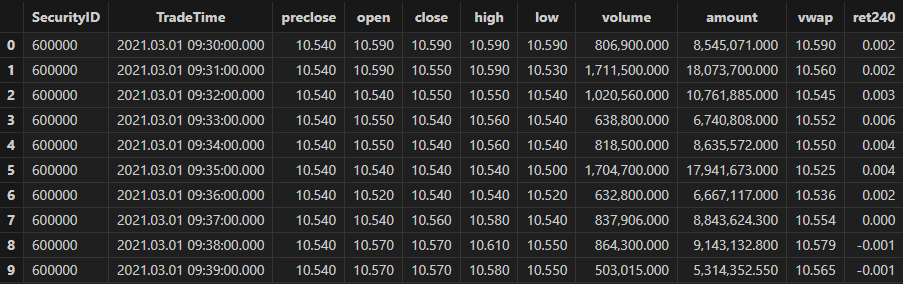
3.2.2 模型训练
与日频场景相同,创建 Shark GPLearnEngine。由于 Alpha 101 和 Alpha 191 为日频因子表达式,分钟频场景并不保证有效,这里不设置 initProgram 参数,而由 Shark 直接生成指定数量的初始种群。在适应度函数方面,使用 Shark 自带的斯皮尔曼相关系数作为适应度进行计算。
trainX = dropColumns!(trainData.copy(), ["TradeTime", "ret240"]) // 训练数据自变量
trainY = trainData["ret240"] // 训练数据因变量
trainDate = trainData["TradeTime"] // 训练数据时间信息
// 配置算子库
functionSet = ["add", "sub", "mul", "div", "sqrt", "reciprocal", "mavg", "msum", "mstdp", "mmin", "mmax", "mimin", "mimax","mcorr", "mrank", "mfirst"]
// 创建 GPLearnEngine 引擎
engine = createGPLearnEngine(trainX,trainY, // 训练数据
fitnessFunc="spearmanr", // 适应度函数
groupCol="SecurityID", // 分组列: 按 SecurityID 分组滑动
seed=42, // 随机数种子
populationSize=1000, // 种群规模
generations=5, // 进化次数
tournamentSize=20, // 锦标赛规模, 表示生成下一代公式时,参与竞争的公式数量
functionSet=functionSet, // 算子库
initProgram=NULL, // 初始种群
minimize=false, // false表示最大化适应度
initMethod="half", // 初始化方法
initDepth=[3, 5], // 初始公式树种群深度
restrictDepth=true, // 是否严格限制树的深度
windowRange=[30,60,120,240,480], // 窗口大小范围
constRange=0, // 0表示公式禁止额外生成常量
parsimonyCoefficient=0.8, // 公式复杂度惩罚系数
crossoverMutationProb=0.8,
subtreeMutationProb=0.1,
hoistMutationProb=0.02,
pointMutationProb=0.02,
deviceId=0 // 指定使用的设备ID
)模型配置完成后,即可调用 gpFit 函数进行模型训练,并返回适应度前 programNum 的因子公式。
// 训练模型,挖掘因子
programNum=30
timer res = engine.gpFit(programNum)
// 查看挖掘结果
resShark GPLearn 返回适应度较优的因子结果表如下所示:
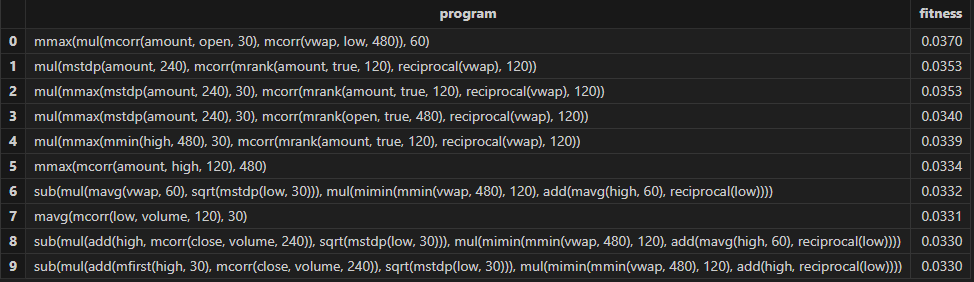
3.2.3 因子评价
模型训练完成后,可以用 gpPredict 函数进行因子计算。
allX = dropColumns!(allData.copy(), ["TradeTime", "ret240"]) // 所有数据自变量
// 计算所有因子值
factorValues = gpPredict(engine, allX, programNum=programNum, groupCol="SecurityID")
factorList = factorValues.colNames() // 因子列表
totalData = table(allData, factorValues)使用 3.1.3 章节中的单因子评价函数,执行因子评价函数并查看结果:
/* 单因子分析
rankICRes: 查看因子 rankIC 明细表
quantileRes: 查看分层收益率最终结果表
rankICStats: 查看 rankIC 分析表
*/
// 单因子分析
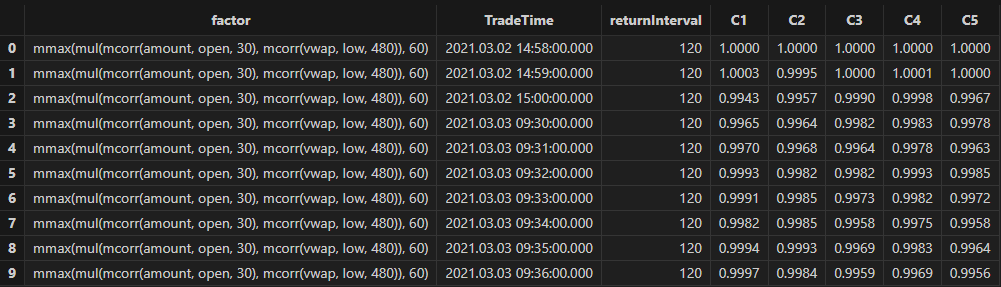
rankICRes, quantileRes, rankICStats = analysisFactors(totalData, factorList, returnIntervals=[120, 240, 480, 720, 1200], quantiles=[0.0, 0.2, 0.4, 0.6, 0.8, 1.0], splitDay=splitDay)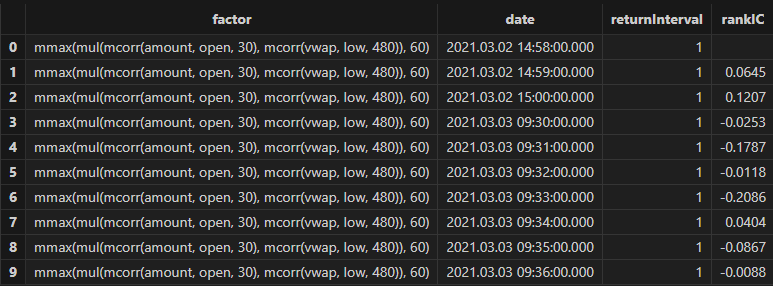

3.2.4 结果可视化
运行以下代码查看 Shark GPLearn 返回一个分钟频优选因子的分钟频 RankIC 与累计 RankIC 结果:
// 分钟频 RankIC 与累计 RankIC 可视化
factorName = factorList[0] // 选取展示的因子
retInterval = 240 // 选取展示的持仓周期
sliceData = select date, rankIC, cumsum(RankIC) as cumRankIC from rankICRes where factor=factorName and returnInterval=retInterval
plot(sliceData[`rankIC`cumRankIC], sliceData[`date], extras={multiYAxes: true})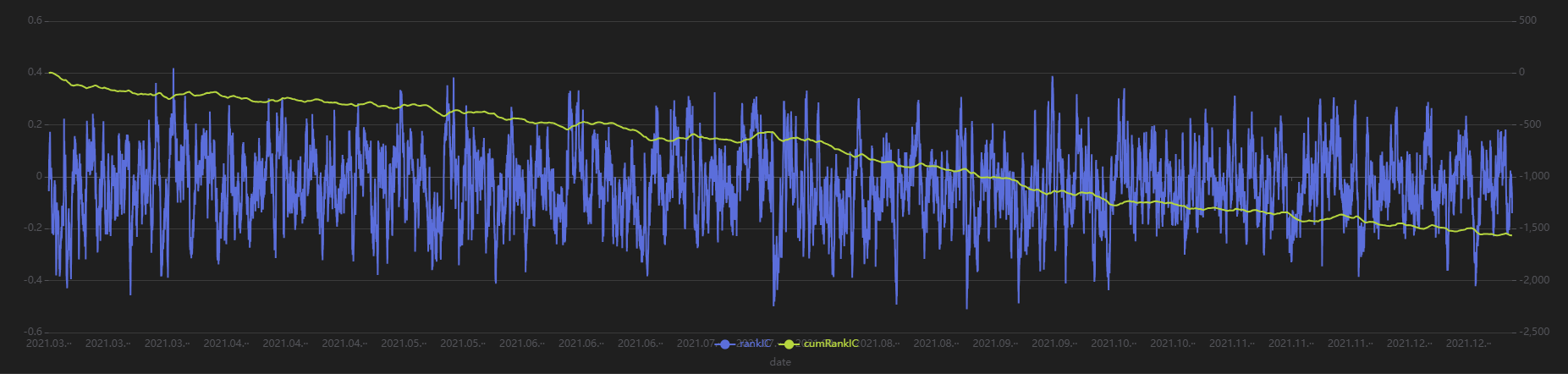
从上图可以发现,该分钟频因子大部分时间内的 RankIC 都 <0,累计 RankIC 呈现稳定向下的态势,说明该因子对于未来 240 分钟的区间收益率具有较好的预测效果。
运行以下代码查看 Shark GPLearn 返回的分钟频优选因子的不同分钟频区间收益率下的 RankIC 结果:
// rankIC 均值可视化
sliceData = select * from rankICStats where factor=factorName
plot(sliceData[`rankIC`trainRankIC`testRankIC], sliceData[`returnInterval])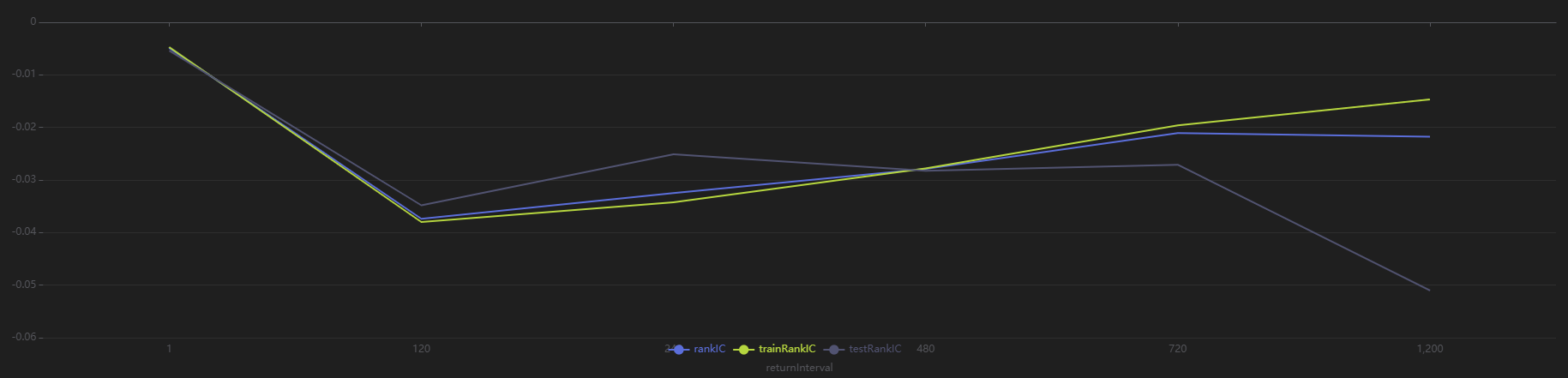
从上图可以看出,在所有样本区间内,该因子对于未来 120 与 240 分钟的收益率预测效果好于其他时间。运行以下代码查看每 240 分钟按第 1 分钟的因子值分组回测得到的分层收益率,该因子最终分层收益率从大到小排序呈现 1-2-3-4-5,符合 RankIC 为负的结果,说明该因子在 240 分钟频段调仓分层效果较为理想。
// 分层收益率可视化
sliceData = select * from quantileRes where factor=factorName and returnInterval=retInterval
plot(sliceData[columnNames(sliceData)[3:]],sliceData[`TradeTime]) 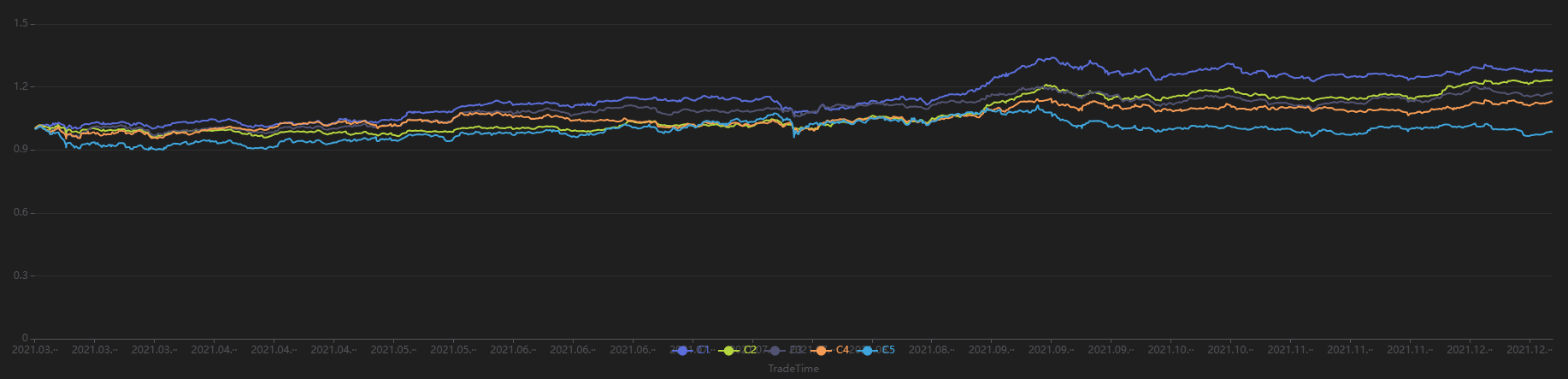
3.3 降频因子挖掘
本章节使用分钟频的 K 线作为训练数据;使用标的列和日期列作为降频列;使用日频的个股 20 日后收益率作为训练目标;以此进行从分钟频输入到日频输出的降频因子挖掘。
3.3.1 数据准备
这里依然利用分钟频因子挖掘所使用的数据,进行降频挖掘得出日频因子结果,并进行因子评价与可视化。同样设定训练集范围为 2021-03-01 至 2021-10-31 期间的交易日,测试集范围为 2021-11-01 至 2021-12-31 期间的交易日。
def processData(splitDay=2021.11.01){
// 数据源: 这里选择从 csv 读取, 需要用户根据实际情况修改文件路径
fileDir = "/home/fln/DolphinDB_V3.00.4/demoData/MinuteKBar.csv"
colNames = ["SecurityID","TradeTime","preclose","open","high","low","close","volume","amount"]
colTypes = ["SYMBOL","TIMESTAMP","DOUBLE","DOUBLE","DOUBLE","DOUBLE","DOUBLE","INT","DOUBLE"]
t = loadText(fileDir, schema=table(colNames, colTypes))
// 获取训练特征: 训练特征需要 FLOAT / DOUBLE 类型; 且训练数据最好根据分组列进行排序
data =
select SecurityID,
date(TradeTime) as TradeDate, // 日期列
TradeTime, // 时间列
preclose, // 昨收价
open, // 开盘价
close, // 收盘价
high, // 最高价
low, // 最低价
double(volume) as volume, // 成交量
amount, // 成交额
nullFill(ffill(Amount \ Volume), 0.0) as vwap,// 成交均价
move(close,-241*20)\close-1 as ret20 // 未来20日收益率
from t context by SecurityID order by SecurityID, TradeTime
data = select * from data where ret20!=NULL order by SecurityID, TradeTime
// 划分训练集
days = distinct(data["TradeTime"])
trainDates = days[days<=splitDay]
trainData = select * from data where TradeTime in trainDates order by SecurityID, TradeTime
// 划分测试集
testDates = days[days>splitDay]
testData = select * from data where TradeTime in testDates order by SecurityID, TradeTime
return data, trainData, testData
}
splitDay = 2021.11.01 // 训练集和测试集的分割点
allData, trainData, testData = processData(splitDay) // 所有数据, 训练数据, 测试数据3.3.2 模型训练
这里与分钟频和日频的场景都不同,由于输入和输出的数据频率发生了变化,需要提前指定降频列,并将降频后的因变量列传参入 Shark GPLearn Engine。需要注意的是,输入的因变量是降频后的结果。因此,输入的 targetData 的向量长度需要和对 tarinData 根据降频列聚合产生的分组数量一致。本文的降频因子挖掘代码如下所示:
// 分钟频输入
trainX = dropColumns!(trainData.copy(),`ret20`TradeTime)
// 日频输出
trainDailyData = select last(ret20) as `ret20 from trainData group by SecurityID, TradeDate
trainY = trainDailyData["ret20"]
trainDate = trainDailyData["TradeDate"] // 训练数据时间信息
// 创建 GPLearnEngine 引擎
engine = createGPLearnEngine(trainX,trainY, // 训练数据
fitnessFunc="spearmanr", // 适应度函数
dimReduceCol=["SecurityID", "TradeDate"], // 聚合列:按 TradeDate 列降频
groupCol="SecurityID", // 分组列: 按 SecurityID 分组滑动
seed=999, // 随机数种子
populationSize=1000, // 种群规模
generations=4, // 进化次数
tournamentSize=20, // 锦标赛规模, 表示生成下一代公式时,参与竞争的公式数量
minimize=false, // false表示最大化适应度
initMethod="half", // 初始化方法
initDepth=[3, 6], // 初始公式树种群深度
restrictDepth=true, // 是否严格限制树的深度
windowRange=int([0.1, 0.2, 0.3, 0.4, 0.5, 0.8, 1, 2, 5]*241), // 窗口大小范围
constRange=0, // 0表示公式禁止额外生成常量
parsimonyCoefficient=0.8, // 公式复杂度惩罚系数
crossoverMutationProb=0.8,
subtreeMutationProb=0.1,
hoistMutationProb=0.02,
pointMutationProb=0.02,
deviceId=0 // 指定使用的设备ID
)模型配置完成后,即可调用 gpFit 函数进行模型训练,并返回适应度前 programNum 的因子公式。
// 训练模型,挖掘因子
programNum = 20
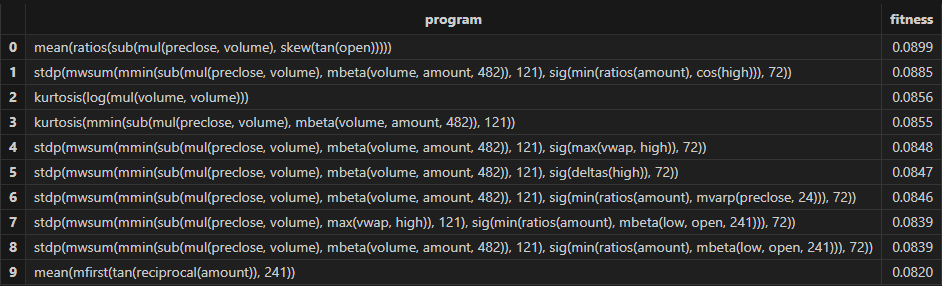
timer res = engine.gpFit(programNum)
// 查看挖掘结果
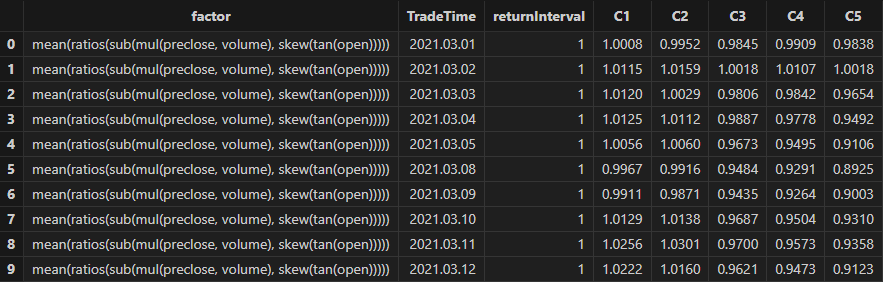
resShark GPLearn 返回适应度较优的因子结果表如下所示:
3.3.3 因子评价
模型训练完成后,可使用 gpPredict 函数进行因子计算。对于降频因子,需要在
gpPredict 中指定 dimReduceCol,即训练时的降频列参数。
需要注意的是,gpPredict 输出的行数与输入数据相同,而非最终的降频结果,实际上只有前 n 行数据是有效的,其中
n 等于最终分组数。因此,在下文代码中,需要对 gpPredict 的输出使用 [0:
rows(totalData)] 进行切片,以获取降频因子结果。
allX = dropColumns!(allData.copy(), ["TradeTime", "ret20"]) // 所有数据自变量
// 计算所有因子值
factorValues = select * from gpPredict(engine, allX, programNum=programNum, groupCol="SecurityID", dimReduceCol=["SecurityID", "TradeDate"])
factorList = factorValues.colNames() // 因子列表
// 输出日频结果
totalData = select last(close) as close from allData group by SecurityID, TradeDate as TradeTime
totalData = table(totalData, factorValues[0:rows(totalData), ])使用 3.1.3 章节中的单因子评价函数,执行因子评价函数并查看结果:
/* 单因子分析
rankICRes: 查看因子 rankIC 明细表
quantileRes: 查看分层收益率最终结果表
rankICStats: 查看 rankIC 分析表
*/
rankICRes, quantileRes, rankICStats = analysisFactors(totalData, factorList, returnIntervals=[1,5,10,20], quantiles=[0.0, 0.2, 0.4, 0.6, 0.8, 1.0], splitDay=splitDay)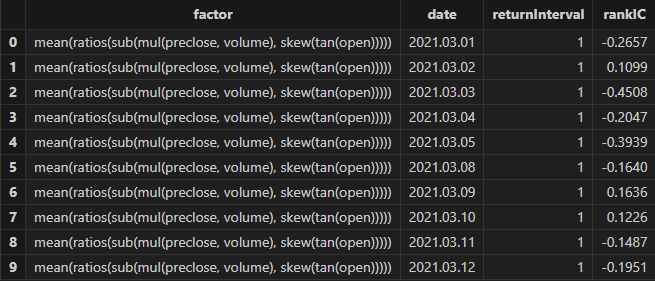

3.3.4 结果可视化
运行以下代码查看 Shark GPLearn 返回的降频频优选因子的日频 RankIC 与累计 RankIC 结果:
// 日频 RankIC 与累计 RankIC 可视化
factorName = factorList[0] // 选取展示的因子
retInterval = 20 // 选取展示的持仓周期
sliceData = select date, rankIC, cumsum(RankIC) as cumRankIC from rankICRes where factor=factorName and returnInterval=retInterval
plot(sliceData[`rankIC`cumRankIC], sliceData[`date], extras={multiYAxes: true})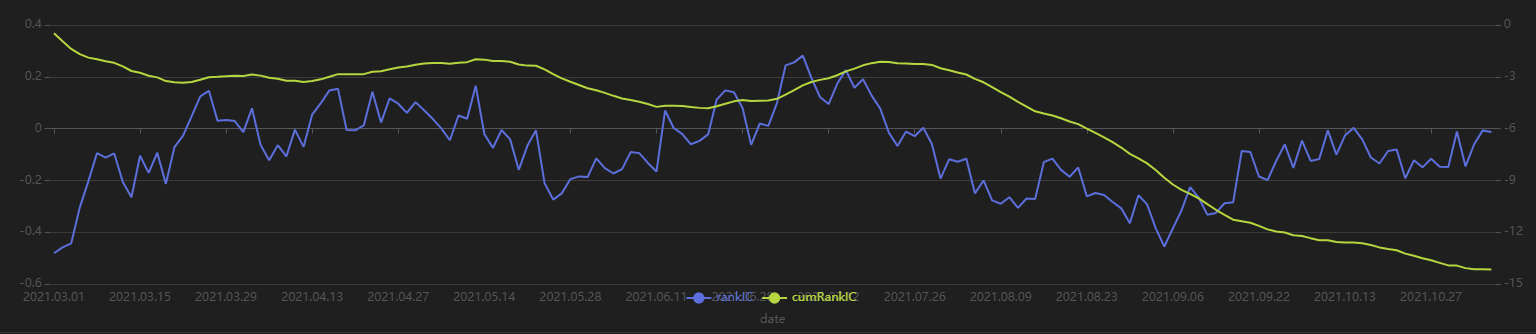
从上图可以发现,该分钟频因子大部分时间内的 RankIC 都 <0,累计 RankIC 呈现稳定向下的态势,说明该因子对于未来 20日 的区间收益率具有较好的预测效果。
运行以下代码查看 Shark GPLearn 返回适应度最佳因子的不同日频区间收益率下的 RankIC 结果,可以发现,该因子对于未来 1~30 日收益率均有较好的预测能力:
// rankIC 均值可视化
sliceData = select * from rankICStats where factor=factorName
plot(sliceData[`rankIC`trainRankIC`testRankIC], sliceData[`returnInterval])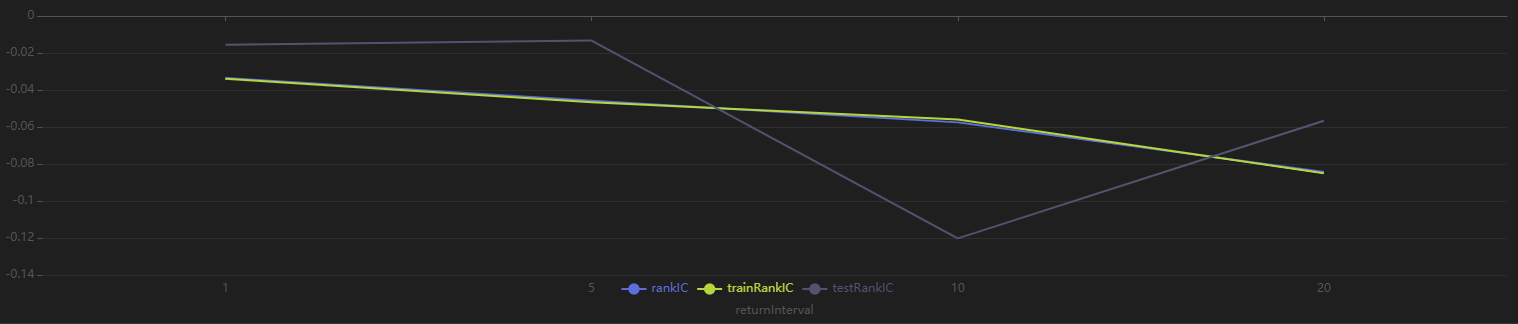
运行以下代码查看每 20 个交易日按第一天的因子值分组回测得到的分层收益率。从下图可以发现分层回测的整体结果与 IC 法的结果一致——该因子利用未来 20 日区间收益率计算的 IC 值显著为负,使用 20 日调仓周期分层回测发现:因子值最高的分组(分组 5)整体收益最低,因子值最低的分组(分组 1)整体收益最高,组间分层明显,说明该因子表现优良。
// 分层收益率可视化
sliceData = select * from quantileRes where factor=factorName and returnInterval=retInterval
plot(sliceData[columnNames(sliceData)[3:]],sliceData[`TradeTime]) 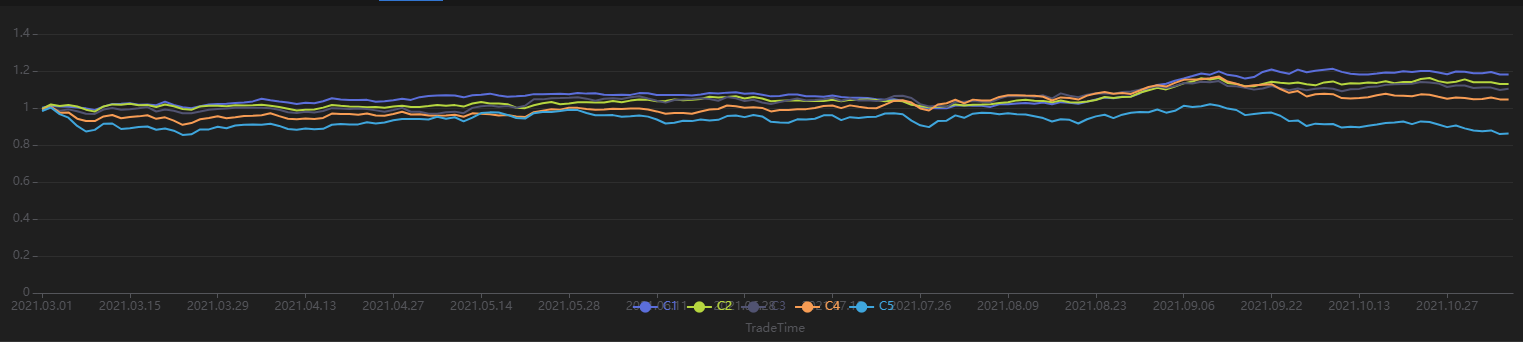
3.4 进阶:自动因子挖掘
3.4.1 自动因子挖掘方法介绍
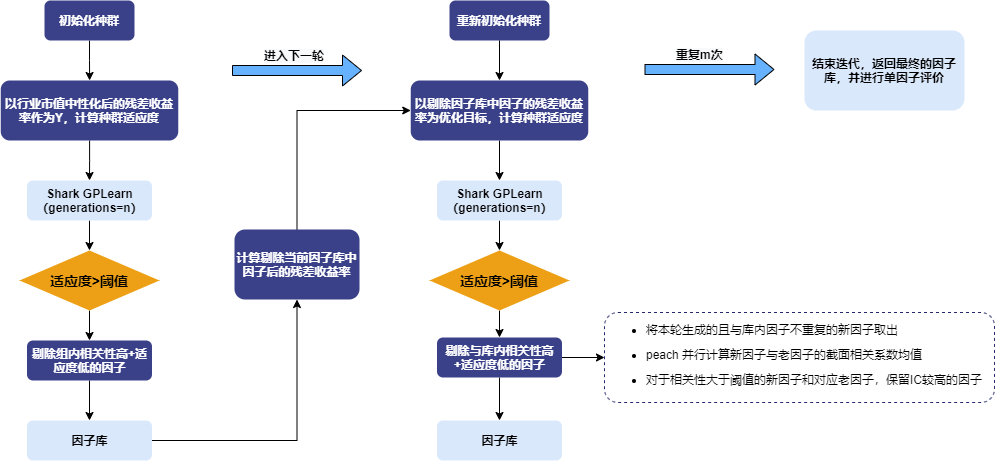
本文使用的自动因子挖掘方法,是以每一轮中挖掘解释收益率的增量信息为目标。在第一轮 Shark GPLearn 因子挖掘时,以剔除风格因子(对数化市值、行业)的残差收益率作为预测目标,利用因子值与残差收益率截面相关系数的均值作为因子适应度。新因子经过适应度以及相关性筛选后进行入库,并将被替换的老因子进行出库,使用新一轮挖掘出的因子进行回归得到新一轮的残差收益率。
重复上述步骤,进行多轮因子挖掘。最终,因子库中剩余的因子即为自动因子挖掘方法筛选得到的结果因子。随后,对这些因子进行单因子测试。自动因子挖掘的整体流程图如下所示:
3.4.2 数据准备
在此步骤中,使用日频数据进行因子自动挖掘,以获得日频因子结果。同样设定训练集范围为 2021-03-01 至 2021-10-31 期间的交易日,测试集范围为 2021-11-01 至 2021-12-31 期间的交易日。
这一步中,加入了行业信息和市值信息,对预测目标进行了行业市值中性化处理。
def processData(splitDay){
// 数据源: 这里选择从 csv 读取, 需要用户根据实际情况修改文件路径
fileDir = "/home/fln/DolphinDB_V3.00.4/demoData/DailyKBar.csv"
industryDir = "/home/fln/DolphinDB_V3.00.4/demoData/Industry.csv"
colNames = ["SecurityID","TradeDate","ret20","preclose","open","close","high","low","volume","amount","vwap","marketvalue","turnover_rate","pctchg","PE","PB"]
colTypes = ["SYMBOL","DATE","DOUBLE","DOUBLE","DOUBLE","DOUBLE","DOUBLE","DOUBLE","INT","DOUBLE","DOUBLE","DOUBLE","DOUBLE","DOUBLE","DOUBLE","DOUBLE"]
t = loadText(fileDir, schema=table(colNames, colTypes))
// 获取训练特征: 训练特征需要 FLOAT / DOUBLE 类型; 且训练数据最好根据分组列进行排序
data =
select SecurityID, TradeDate as TradeTime,
preclose, // 昨收价
open, // 开盘价
close, // 收盘价
high, // 最高价
low, // 最低价
double(volume) as volume, // 成交量
amount, // 成交额
pctchg, // 涨跌幅
vwap, // 成交均价
marketvalue, // 总市值
turnover_rate, // 换手率
double(1\PE) as EP, // 盈利收益率
double(1\PB) as BP, // 账面市值比
ret20, // 未来20日收益率
log(marketvalue) as marketvalue_ln // 总市值对数
from t order by SecurityID, TradeDate
// 行业数据
industryData = select SecurityID,
int(left(strReplace(IndustryCode,"c",""),2)) as Industry
from loadText(industryDir)
context by SecurityID
order by UpdateDate
limit -1; // 读取最新所有股票的申万一级行业数据
industryData = oneHot(industryData, "Industry")
data = lj(data, industryData, "SecurityID")
industryCols = columnNames(industryData)[1:]
// 行业市值中性化
neutralCols = [`marketvalue_ln]<-industryCols // 对数市值列+行业列
ols_params = ols(data[`ret20], data[neutralCols], intercept=false) // 行业one-hot等于截距项, 所以这里不能添加截距项
data[`ret20] = residual(data[`ret20], data[neutralCols], ols_params, intercept=false)
dropColumns!(data, neutralCols) // 行业+市值中性化后删除对数市值+行业数据
// 划分训练集
days = distinct(data["TradeTime"])
trainDates = days[days<=splitDay]
trainData = select * from data where TradeTime in trainDates order by SecurityID, TradeTime
// 划分测试集
testDates = days[days>splitDay]
testData = select * from data where TradeTime in testDates order by SecurityID, TradeTime
return data, trainData, testData
}3.4.3 模型训练(小循环)
仿照 3.1 日频因子挖掘 的章节,将模型设置的代码封装为函数,以便于后续的循环调用。本章节的示例代码如下:
// 修改适应度函数为自定义函数: 计算 rank IC
def myFitness(x, y, groupCol){
return abs(mean(groupby(spearmanr, [x, y], groupCol)))
}
def setModel(trainData, innerIterNum){
trainX = dropColumns!(trainData.copy(), ["TradeTime", "ret20"]) // 训练数据自变量
trainY = trainData["ret20"] // 训练数据因变量
trainDate = trainData["TradeTime"] // 训练数据时间信息
// 配置算子库
functionSet = ["add", "sub", "mul", "div", "sqrt", "reciprocal", "mprod", "mavg", "msum", "mstdp", "mmin", "mmax", "mimin", "mimax","mcorr", "mrank", "mfirst"]
// 创建 GPLearnEngine 引擎
engine = createGPLearnEngine(trainX,trainY, // 训练数据
groupCol="SecurityID", // 分组列: 按 SecurityID 分组滑动
seed=99, // 随机数种子
populationSize=1000, // 种群规模
generations=innerIterNum, // 进化次数
tournamentSize=20, // 锦标赛规模, 表示生成下一代公式时,参与竞争的公式数量
functionSet=functionSet, // 算子库
minimize=false, // false表示最大化适应度
initMethod="half", // 初始化方法
initDepth=[2, 4], // 初始公式树种群深度
restrictDepth=true, // 是否严格限制树的深度
windowRange=[5,10,20,40,60], // 窗口大小范围
constRange=0, // 0表示公式禁止额外生成常量
parsimonyCoefficient=0.05, // 复杂度惩罚系数
crossoverMutationProb=0.6, // crossover的概率
subtreeMutationProb=0.01, // subtree的概率
hoistMutationProb=0.01, // hoist变异的概率
pointMutationProb=0.01, // point变异的概率
deviceId=0, // 指定使用的设备ID
verbose=false, // 是否输出每轮训练情况
useAbsFit=false // 在计算适应度时是否取绝对值。
)
// 设置适应度函数
setGpFitnessFunc(engine, myFitness, trainDate)
return engine
}3.4.4 自动挖掘(大循环)
针对每个因子表达式,先定义因子 IC 值的计算方法和因子间相关系数的计算方法,用于后续自动过滤因子表达式。
// 因子相关性计算
def corrCalFunc(data, timeCol, factor1Col, factor2Col){
// 计算每天的因子相关性
t = groupby(def(x,y):corr(zscore(x), zscore(y)),[data[factor1Col],data[factor2Col]], data[timeCol]).rename!(`time`corr)
return abs(avg(t["corr"]))
}
// 因子IC值计算
def icCalFunc(data, timeCol, factorCol, retCol){
t = groupby(def(x, y):spearmanr(zscore(x), y),[data[factorCol],data[retCol]], data[timeCol]).rename!(`time`ic)
return abs(mean(t["ic"]))
}对于计算得到的评价指标(因子 IC 值和因子间的相关系数),定义一个自动筛选因子表达式的逻辑。本章节实现的过滤逻辑:保留因子相关性小于 0.7 的因子表达式;如果出现相关性超过 0.7 的情况,则保留 IC 值最高的因子表达式,其余表达式剔除。
// 定义删除相关性超过阈值的因子的方法
def getDeleteFactorList(factorsPair, corrThreshold, factorICInfo){
factorInfo = lj(factorsPair, factorICInfo, `newFactor, `factor)
deleteList = array(STRING, 0)
do{
corrRes = select count(*) as num, max(ic) as ic from factorInfo where factorCorr>=corrThreshold group by newFactor order by num, ic
if(corrRes.rows()==0){ // 如果不存在相关性大于阈值的因子, 结束循环
break
}else{ // 对于相关性大于阈值的因子,选择其中 ic 值高的保留
deleteFactor = corrRes["newFactor"][0]
deleteList.append!(deleteFactor)
delete from factorInfo where newFactor=deleteFactor or allFactor=deleteFactor
}
}while(true)
return deleteList
}结合 3.4.3 章节的日频因子挖掘模型,实现一套自动挖掘流程:
-
通过模型挖掘新的因子
-
对于通过 GPLearn 模型挖掘出来的批量因子,根据指定的筛选逻辑,保留其中优质因子
-
从训练目标中,剔除新增因子的影响
-
循环,继续挖掘新的因子
// 训练模型(大循环)
def trainModel(data, outerIterNum, innerIterNum, returnNum, icThreshold, corrThreshold){
// 训练数据自变量
trainData = data
trainX = dropColumns!(trainData.copy(), ["TradeTime", "ret20"])
// 设置因子表 (公式)
factorLists = table(1:0, ["iterNum", "factor", "IC"], [INT, STRING, DOUBLE])
// 设置因子表 (因子值)
factorValues = select SecurityID, TradeTime, ret20 from trainData
// 循环多轮挖掘
for(i in 0:outerIterNum){ // i = 0
print("第"+string(i+1)+"轮大循环开始")
// 设置模型
engine = setModel(trainData, innerIterNum)
// 训练模型
timer fitRes = engine.gpFit(returnNum)
// 计算所有因子值
timer newfactorValues = gpPredict(engine, trainX, programNum=returnNum, groupCol="SecurityID")
newfactorList = newfactorValues.colNames()
allfactorList = factorValues.colNames()
// 删除重复因子
newfactorValues.dropColumns!(newfactorList[newfactorList in allfactorList])
// 对新增因子计算IC值
factorValues = table(factorValues, newfactorValues)
timer factorICInfo = select *, peach(icCalFunc{factorValues, "TradeTime", , "ret20"}, factor) as ic
from table(newfactorList as factor)
// 删除不满足 ic 阈值的因子
deleteFactors = exec factor from factorICInfo where ic<=icThreshold
dropColumns!(factorValues, deleteFactors)
newfactorList = newfactorList[!(newfactorList in deleteFactors)]
// 计算新增因子和原始因子的相关性
allFactorList = factorValues.colNames()
allFactorList = allFactorList[!(allFactorList in ["SecurityID", "TradeTime", "ret20"])]
factorsPair = cj(table(newfactorList as newFactor), table(allFactorList as allFactor))
timer factorsPair = select *, peach(corrCalFunc{factorValues, "TradeTime"}, newFactor, allFactor) as factorCorr from factorsPair where newFactor!=allFactor
// 删除相关性大于阈值的因子
deleteFactors = getDeleteFactorList(factorsPair, corrThreshold, factorICInfo)
dropColumns!(factorValues, deleteFactors)
newfactorList = newfactorList[!(newfactorList in deleteFactors)]
// 将满足条件的因子写入因子表(公式)
newFactorInfo = table(take(i+1, size(newfactorList)) as iterNum, newfactorList as factor)
factorLists.append!(lj(newFactorInfo, factorICInfo, `factor))
print("第"+string(i+1)+"轮大循环新增因子"+string(size(newfactorList))+"个")
// 对预测目标里删除新增因子的影响
if(size(newfactorList)>0){
ols_params = ols(trainData[`ret20], factorValues[newfactorList], intercept=true)
trainData[`ret20] = residual(trainData[`ret20], factorValues[newfactorList], ols_params, intercept=true)
}else{
break
}
}
return factorLists
}本文进行测试的自动因子挖掘的函数参数配置如下:
| 参数含义 | 参数名称 | 参数设置 |
|---|---|---|
| 重置种群迭代次数(大循环) | outerIterNum | 3 |
| 遗传算法迭代次数(小循环) | innerIterNum | 5 |
| 因子表达式 IC 阈值 | icThreshold | 0.03 |
| 因子表达式相关系数均值阈值 | corrThreshold | 0.7 |
| 单次模型返回因子的数量 | returnNum | 100 |
outerIterNum = 3 // 重置种群迭代次数(大循环)
innerIterNum = 5 // 遗传算法迭代次数(小循环)
icThreshold = 0.03 // 因子表达式 ic 阈值
corrThreshold = 0.7 // 与库内已有因子的截面相关系数均值阈值
returnNum = 100 // 每次返回适应度最优因子的数量
allData = processData() // 所有数据
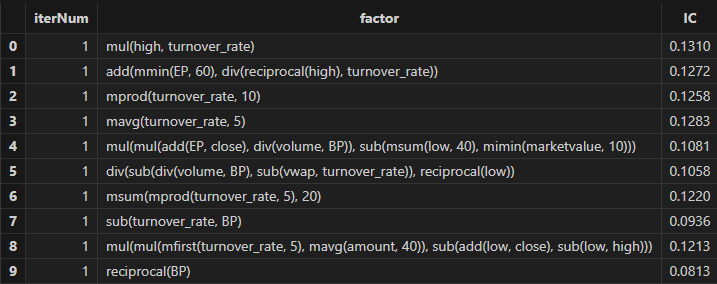
timer res = trainModel(allData, outerIterNum, innerIterNum, returnNum, icThreshold, corrThreshold)运行后,可以得到一批因子公式,如下图:
4. 性能对比
为了进一步地展现 Shark GPLearn 的强大性能,本文在相同测试环境与测试条件下,对于 Shark GPLearn 、 Python GPLearn 与 Python Deap 进行了性能对比。
4.1 测试条件设置
考虑到 Shark GPLearn 的参数较为丰富,本次只设置 Shark GPLearn、Python GPLearn 与 Python Deap 共有的参数。
| 训练参数 | Shark GPLearn | Python GPLearn | Deap | 参数值 |
|---|---|---|---|---|
| 目标函数 | fitnessFunc=”pearson” | metric=fitness.make_fitness(…) | toolbox.register(“evaluate”, …) | 自定义适应度函数 |
| 迭代次数 | generations | generations | ngen | 5 |
| 种群规模 | populationSize | population_size | population | 1000 |
| 锦标赛规模 | tournamentSize | tournament_size | tournsize | 20 |
| 常数项 | constRange=0 | const_range=None | 不设置addTerminal | 按前述参数描述取值 |
| 节俭系数 | parsimonyCoefficient | parsimony_coefficient | 无 | 0.05 |
| 交叉变异概率 | crossoverMutationProb | p_crossover | 无 | 0.6 |
| 子树变异概率 | subtreeMutationProb | p_subtree_mutation | 无 | 0.01 |
| Hoist变异概率 | hoistMutationProb | p_hoist_mutation | 无 | 0.01 |
| Point变异概率 | pointMutationProb | p_point_mutation | 无 | 0.01 |
| 初始化策略 | initMethod=”half” | init_method=”half and half ” | gp.genHalfAndHalf | 按前述参数描述取值 |
| 初始公式树深度 |
initDepth=[2, 4] restrictDepth=false |
init_depth=(2, 4) |
min_=2 max_=4 |
按前述参数描述取值 |
| 并行度 | 无 | njobs=8(独有) | 无 | 按前述参数描述取值 |
在特征方面,使用以下特征作为训练特征;训练目标列为 ret20(标的未来 20 日的区间收益率)。
| 训练特征 | 含义 | 训练特征 | 含义 |
|---|---|---|---|
| preclose | 前收盘价 | pctchg | 收盘价变动 |
| open | 开盘价 | vwap | 平均价格 |
| close | 收盘价 | marketvalue | 总市值 |
| high | 最高价 | turnover_rate | 换手率 |
| low | 最低价 | EP | 市盈率的倒数 |
| volume | 成交量 | BP | 市净率的倒数 |
| amount | 成交金额 |
在自定义适应度函数方面,统一使用因子值与 ret20 的 Pearson 相关系数。在数据与算子层面上,统一使用 2020-08-12 至 2022-12-31 之间的全部交易日作为训练集,2023-01-01 至 2023-06-19 的全部交易日作为测试集。标的范围为3002只股票,训练集样本量为 1744162 条,测试集样本量为 333222 条。
4.2 测试结果
| 软件 | 版本 | 训练耗时(s) |
|---|---|---|
| DolphinDB Shark | 3.00.4 2025.09.05 LINUX_ABI x86_64 | 6.3 |
| Python GPLearn | 3.12.7 | 189 |
| Python Deap | 3.12.7 | 1102 |
测试结果显示,Shark 相较于 Python GPLearn 和 Python DEAP 的性能分别提高了 30.0 倍和 174.9 倍。
从功能上而言,Shark 相对于 Python GPLearn 与 Python Deap具有更丰富的功能,如支持:
-
设置
restrictDepth=true全程限制公式树深度 -
设置
groupCol使得适应度函数支持分组运算 -
设置
windowRange指定窗口函数的大小范围 -
更丰富的算子集
functionSet运算支持 -
更便捷的表达式字符串解析调用方式:
sqlColAlias+parseExpr函数
4.3 测试环境配置
安装 DolphinDB server,配置为集群模式。本次测试所涉及到的硬件环境和软件环境如下:
-
硬件环境
硬件名称 配置信息 内核 3.10.0-1160.88.1.el7.x86_64 CPU Intel(R) Xeon(R) Gold 5220R CPU @ 2.20GHz GPU NVIDIA A30 24GB(1块) 内存 512GB
-
软件环境
软件名称 版本及配置信息 操作系统 CentOS Linux 7 (Core) DolphinDB
server 版本:3.00.4 2025.09.05 LINUX_ABI x86_64 license 限制:16 核 128 GB
5. 总结
本文基于 DolphinDB CPU-GPU 异构平台 Shark 的 GPLearn 遗传算法因子挖掘功能,完整实现了日频因子挖掘、分钟频因子挖掘、降频因子挖掘以及自动因子挖掘四大应用场景。Shark GPLearn 利用 DolphinDB 强大的计算性能和灵活的数据处理能力,能够帮助用户更快地挖掘出更多更优质的因子表达式。
未来,Shark GPLearn 将进一步扩展对 DolphinDB 内置函数算子的支持,并且允许用户通过脚本语言定义更加灵活的自定义函数算子,从而更好的满足不同应用场景下的需求。
6. 常见问题(FAQ)
1. 单因子测试中常用哪些方法?
单因子测试方法通常可以分为 ICIR 法、回归法与分层回测法三种,本文主要使用了 ICIR 法与分层回测法进行单因子测试。
若遗传算法生成的因子表达式满足以下条件,则说明该因子具有较强的线性收益率预测能力:
-
在训练期与测试期的 RankIC 值符号相同且绝对值大于阈值
-
分层回测收益: Top 组 > Middle 组 > Bottom 组且 RankIC 稳定为正
-
分层回测收益: Top 组 < Middle 组 < Bottom 组且 RankIC 稳定为负
若遗传算法生成的因子表达式满足以下条件,则说明该因子的收益率预测具有非线性的特征:
-
分层回测的结果显示 Middle 组收益显著高于 Top 组与 Bottom 组
2. 自动因子挖掘中如何修改相关配置,如何自定义因子选择与剔除的判断逻辑?
在应用案例自动因子挖掘.dos 的文件开头,修改 outerIterNum(重置种群迭代次数)、innerIterNum(遗传算法迭代次数)、icThreshold(因子表达式适应度阈值)以及 corrThreshold(与库内已有的因子截面相关系数的均值阈值),即可调整自动因子挖掘的相关配置。
附录
- 代码适用版本:3.00.4 2025.09.09 LINUX_ABI x86_64 (Shark)
- 代码文件:
