响应式无状态引擎
响应式无状态引擎的核心设计目的是处理数据流中存在的依赖关系。当某个数据的值依赖于其他一个或多个数据的最新状态时,此引擎能够确保在任何被依赖的数据更新后,所有直接或间接依赖于此数据的计算结果都会被自动、实时地重新计算并输出。整体流程和 excel 的触发式计算很相似。
例如,一个衍生品的价格(如期权)可能依赖于标的资产的最新价、波动率等多个基础指标。当任何一个基础指标变动时,都需要立即重新计算衍生品价格。
如果通过定义函数来计算这些指标,当指标之间的依赖关系非常复杂(例如 A 指标影响 B,B 又影响 C)时,维护一个依赖关系图会让开发者很头疼。在响应式无状态引擎中,用户无需手动构建或维护依赖关系图,也无需编写触发判断和状态传播代码,只需以声明式语法定义计算规则,系统便会自动、高效且可靠地处理数据的流动与计算。这不仅大幅提升了开发效率、降低了代码复杂度和出错风险,更提供了经过深度优化的高性能计算能力,并实现与流处理框架的无缝集成,带来开箱即用的体验。
响应式无状态引擎由函数 createReactiveStatelessEngine 创建,其语法如下:
createReactiveStatelessEngine(name, metrics, outputTable, [snapshotDir],
[snapshotIntervalInMsgCount])
其参数的详细含义可以参考:createReactiveStatelessEngine。
计算规则
每当引擎注入一批数据时,它会根据参数 metrics 中定义的依赖关系,将任何直接依赖或间接依赖这批数据的指标输出。每次输出的条数等于直接或间接依赖这批数据的变量个数。即使这个变量的值没有改变,也会被输出。
接下来将由浅入深的讲解下如何使用响应式无状态引擎实现投资组合的风险的监控。
应用示例1 - 股票总价值实时更新
计算股票 A 的总价值的计算公式为:股票 A 持仓价值 = 股票 A 最新价 * 持仓数量
在 excel 中实现 (amount= stock_A.price * stock_A.volume):
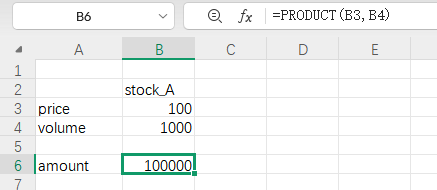
使用响应式无状态引擎实现的代码如下:
// 1. 创建输出表
outputTable = table(1:0, `product`metric`value, [STRING, STRING, DOUBLE])
// 2. 定义依赖关系 (Metrics)
metrics = array(ANY, 0)
// 规则1:计算股票A的价值
// 该引擎的值都是用 rowname:colname 的形式来进行表示的
metricA = dict(STRING, ANY)
metricA["outputName"] = `stock_A:`amount // 表示输出结果
metricA["formula"] = <price * volume> // 定义计算公式,其中prce 和 volume 在下面有定义
metricA["price"] = `stock_A:`price // 定义 price 的值
metricA["volume"] = `stock_A:`volume // 定义 volume 的值
metrics.append!(metricA)
// 3. 创建引擎
engine = createReactiveStatelessEngine("portfolioEngine", metrics, outputTable)
// 4. 模拟数据流入
insert into engine values(["stock_A"],["price","volume"],[10])
insert into engine values(["stock_A"],["volume"],[1000])
// 或者:insert into engine values(["stock_A","stock_A"],["price","volume"],[10,1000])输出如下:
| product | metric | value |
|---|---|---|
| stock_A | amount | 10,000 |
应用示例2 - 投资组合总价值实时更新
本节将在示例 1 的基础上实时更新单只股票的价值以及投资组合的总价值。以两只股票为例,计算公式如下:
股票 A 持仓价值 = 股票 A 最新价 * 持仓数量
股票 B 持仓价值 = 股票 B 最新价 * 持仓数量
组合总价值 = 股票 A 持仓价值 + 股票 B 持仓价值
try{dropStreamEngine("portfolioEngine")}catch(ex){}
// 1. 创建输出表(使用键值表,只保留最新状态)
outputTable = keyedTable(`product`metric,1:0, `product`metric`value, [STRING, STRING, DOUBLE])
// 2. 定义依赖关系 (Metrics)
metrics = array(ANY, 0)
// 规则1:计算股票A的价值
metricA = dict(STRING, ANY)
metricA["outputName"] = `stock_A:`amount
metricA["formula"] = <price * volume>
metricA["price"] = `stock_A:`price
metricA["volume"] = `stock_A:`volume
metrics.append!(metricA)
// 规则2:计算股票B的价值
metricB = dict(STRING, ANY)
metricB["outputName"] = `stock_B:`amount
metricB["formula"] = <price * volume>
metricB["price"] = `stock_B:`price
metricB["volume"] = `stock_B:`volume
metrics.append!(metricB)
// 规则3:计算组合总价值 (依赖于前两个规则的结果)
metricAB = dict(STRING, ANY)
metricAB["outputName"] = `portfolio:`amount
metricAB["formula"] = <A_amount + B_amount>
metricAB["A_amount"] = `stock_A:`amount
metricAB["B_amount"] = `stock_B:`amount
metrics.append!(metricAB)
// 3. 创建引擎
engine = createReactiveStatelessEngine("portfolioEngine", metrics, outputTable)
// 4. 模拟数据流入
insert into engine values("stock_A","price",10)
insert into engine values("stock_A","volume",1000)
insert into engine values("stock_B","price",20)
insert into engine values("stock_B","volume",1000)结果如下:
| product | metric | value |
|---|---|---|
| stock_A | amount | 10,000 |
| stock_B | amount | 20,000 |
| portfolio | amount | 30,000 |
应用示例3 - 投资组合的风险监控
持仓价值依赖于实时价格和数量,风险价值(VaR)进一步依赖于持仓价值和波动率,而组合总风险又由各资产的风险价值聚合得出。任何底层市场数据的更新都会自动触发所有直接或间接受影响指标的重新计算。这种自动化的依赖传播机制使得风险经理能够实时掌握投资组合的整体风险状况,并对市场波动做出即时反应。
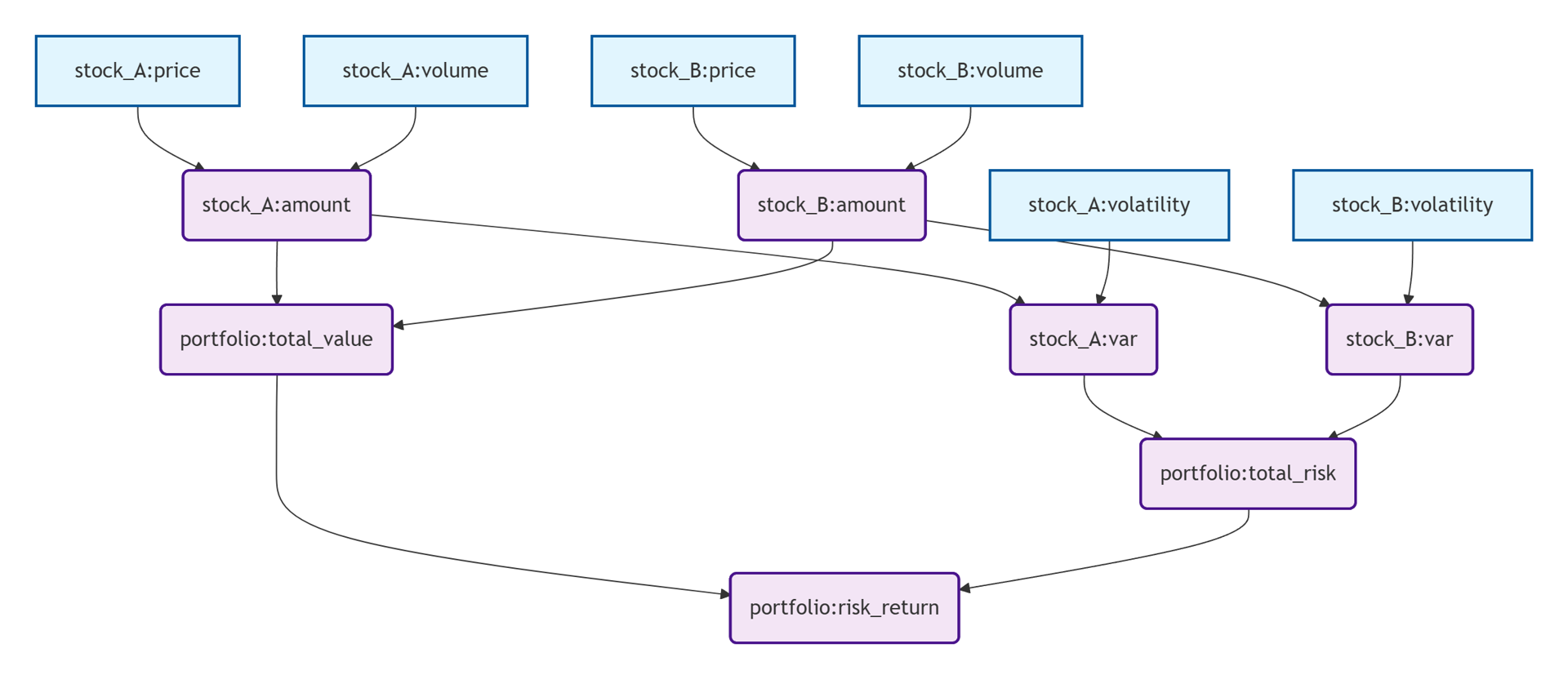
如上图所示,本案例从基础持仓计算出发,通过股价和数量得出个股价值;继而进入风险价值层,结合波动率测算个股潜在损失;随后在组合层聚合价值与风险,并考量资产相关性得出整体风险敞口;最终在顶层生成风险收益率这一核心绩效指标。一共四层计算,每层的计算逻辑如下:
第一层:基础持仓计算
-
股票 A 持仓价值 (stock_A:amount)
-
公式:A_Price * A_Volume
-
依赖:stock_A:price, stock_A:volume
-
业务含义:实时计算持有股票 A 的总市值。
-
-
股票 B 持仓价值 (stock_B:amount)
-
公式:B_Price * B_Volume
-
依赖:stock_B:price, stock_B:volume
-
业务含义:实时计算持有股票 B 的总市值。
-
第二层:风险价值计算
-
股票 A 风险价值 (stock_A:var)
-
公式:A_Amount * A_Volatility * 2.33
-
依赖:stock_A:amount, stock_A:volatility
-
业务含义:在 95% 置信度下(Z 值为 2.33),股票 A 在特定时期内可能的最大损失估计。这是衡量单一资产风险的经典指标。
-
-
股票 B 风险价值 (stock_B:var)
-
公式:B_Amount * B_Volatility * 2.33
-
依赖:stock_B:amount, stock_B:volatility
-
业务含义:衡量股票 B 的潜在最大损失。
-
第三层:投资组合层面计算
-
投资组合总价值 (portfolio:total_value)
-
公式:A_Amount + B_Amount
-
依赖:stock_A:amount, stock_B:amount
-
业务含义:实时计算整个投资组合的总市值。
-
-
投资组合总风险 (portfolio:total_risk)
-
公式:sqrt(A_VaR² + B_VaR² + 2 * 0.3 * A_VaR * B_VaR)
-
依赖:stock_A:var, stock_B:var
-
业务含义:基于风险价值 VaR,考虑资产间相关性(假设相关系数为 0.3)后,计算出的组合整体风险。这比简单相加更准确,因为它考虑了风险分散效应。
-
第四层:综合绩效指标
-
风险收益率 (portfolio:risk_return)
-
公式:Total_Value / Total_Risk
-
依赖:portfolio:total_value, portfolio:total_risk
-
业务含义:这是类似夏普比率的指标,衡量每单位风险所带来的收益。该值越高,说明投资组合的绩效越好,因为用更小的风险获得了更大的收益。
-
具体实现代码如下:
try{dropStreamEngine("riskEngine")}catch(ex){}
// 1. 创建输出表(使用键值表,只保留最新状态)
outputTable = keyedTable(`product`metric, 1:0, `product`metric`value, [STRING, STRING, DOUBLE])
// 2. 定义依赖关系 (Metrics)
metrics = array(ANY, 0)
// 规则1:计算股票A的持仓价值 (amount = price * volume)
metricA = dict(STRING, ANY)
metricA["outputName"] = `stock_A:`amount
metricA["formula"] = <price * volume>
metricA["price"] = `stock_A:`price
metricA["volume"] = `stock_A:`volume
metrics.append!(metricA)
// 规则2:计算股票B的持仓价值 (amount = price * volume)
metricB = dict(STRING, ANY)
metricB["outputName"] = `stock_B:`amount
metricB["formula"] = <price * volume>
metricB["price"] = `stock_B:`price
metricB["volume"] = `stock_B:`volume
metrics.append!(metricB)
// 规则3:计算股票A的风险价值(VaR)
metricAVaR = dict(STRING, ANY)
metricAVaR["outputName"] = `stock_A:`var
metricAVaR["formula"] = <2.33 * amount * volatility>
metricAVaR["amount"] = `stock_A:`amount
metricAVaR["volatility"] = `stock_A:`volatility
metrics.append!(metricAVaR)
// 规则4:计算股票B的风险价值(VaR)
metricBVaR = dict(STRING, ANY)
metricBVaR["outputName"] = `stock_B:`var
metricBVaR["formula"] = <2.33 * amount * volatility>
metricBVaR["amount"] = `stock_B:`amount
metricBVaR["volatility"] = `stock_B:`volatility
metrics.append!(metricBVaR)
// 规则5:计算组合总价值
metricTotalValue = dict(STRING, ANY)
metricTotalValue["outputName"] = `portfolio:`total_value
metricTotalValue["formula"] = <A_amount + B_amount>
metricTotalValue["A_amount"] = `stock_A:`amount
metricTotalValue["B_amount"] = `stock_B:`amount
metrics.append!(metricTotalValue)
// 规则6:计算组合总风险(基于风险价值)
metricTotalRisk = dict(STRING, ANY)
metricTotalRisk["outputName"] = `portfolio:`total_risk
metricTotalRisk["formula"] = <sqrt(A_var*A_var + B_var*B_var + 2 * 0.3 * A_var*B_var)>
metricTotalRisk["A_var"] = `stock_A:`var
metricTotalRisk["B_var"] = `stock_B:`var
metrics.append!(metricTotalRisk)
// 规则7:计算风险收益率
metricRiskReturn = dict(STRING, ANY)
metricRiskReturn["outputName"] = `portfolio:`risk_return
metricRiskReturn["formula"] = <total_value / total_risk>
metricRiskReturn["total_value"] = `portfolio:`total_value
metricRiskReturn["total_risk"] = `portfolio:`total_risk
metrics.append!(metricRiskReturn)
// 3. 创建引擎
engine = createReactiveStatelessEngine("riskEngine", metrics, outputTable)
// 4. 模拟数据流入
// 第一步:输入基础数据 (价格和成交量)
insert into engine values("stock_A", "price", 10.5)
insert into engine values("stock_A", "volume", 1000)
insert into engine values("stock_B", "price", 20.3)
insert into engine values("stock_B", "volume", 500)
// 第二步:输入风险数据
insert into engine values("stock_A", "volatility", 0.15)
insert into engine values("stock_B", "volatility", 0.08)
// 第三步:更新股票A价格,观察连锁反应
insert into engine values("stock_A", "price", 11.2)输出结果如下:
| product | metric | value |
|---|---|---|
| stock_A | amount | 11,200 |
| stock_A | var | 3,914.3999999999996 |
| portfolio | total_value | 21,350 |
| portfolio | total_risk | 4,831.72566853707 |
| portfolio | risk_return | 4.418711132344619 |
| stock_B | amount | 10,150 |
| stock_B | var | 1,891.96 |
