fminSLSQP

fminSLSQP(func, X0, [fprime], [constraints], [bounds], [ftol=1e-6], [epsilon], [maxIter=100])

使用顺序最小二乘编程方法（Sequential Least Squares Programming, SLSQP）找到目标函数的最小值。

func 函数名，表示需要最小化的目标函数。注意：函数返回值须是数值标量类型。

X0 数值类型的标量或向量，表示使目标函数最小化的参数的初始猜测。

fprime 可选参数，函数名，表示计算 func 梯度的函数。如果为空，则使用数值微分方法来获取函数梯度。

constraints 可选参数，字典向量，表示待优化参数需满足的约束条件，每个字典应包含下列成员：

• type：字符串标量，表示约束类型。有两个可选值：'eq'表示等式约束，'ineq'表示不等式约束。

• fun：函数名，表示约束函数。注意：函数返回值须是一个数值标量或向量。

• jac：函数名，表示约束函数 fun 的梯度函数。注意：函数返回值须是一个数值向量或矩阵。

  注意：

  • 假设 fun 返回值的大小为 m，待优化参数的 size 为 n，则 jac 的返回值的形状必须是(n, m)。
  • constraints 中的等式约束（Equality Constraint）的数量不能超过待优化参数的大小。假设待优化参数的大小为 n，constraints 中共有 k 个等式约束函数，constraints 中第 i 个等式约束的约束函数 fun 的返回值大小为 len_i，则应满足：

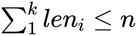
bounds 可选参数，数值矩阵，形状为(N,2)，其中 N 为需要优化的参数数量，即 N=size(X0)。每一行的两个值（min, max），定义了对应参数的边界。

ftol 可选参数，数值标量，正数，表示算法停止时对目标函数值的精度要求，默认值为 1e-6。

epsilon 可选参数，数值标量，正数，表示当使用数值近似方法来求解函数梯度时使用的步长。默认值为 1.4901161193847656e-08。

maxIter 可选参数，非负整数标量，表示最大迭代次数，默认值为 100。

返回一个字典，字典有以下成员：

• xopt：浮点数向量，使目标函数最小化的参数值。

• fopt：浮点数标量，目标函数最小值。fopt=func(xopt)。

• iterations：整数标量，优化过程中执行的总迭代数。

• mode：整数标量，表示算法退出时的状态。mode=0 时表示成功进行优化，取其他值表示算法异常退出，详细说明可参考文档 jacobwilliams - slsqp。

def rosen(x) { 
	N = size(x);
	return sum(100.0*power(x[1:N]-power(x[0:(N-1)], 2.0), 2.0)+power(1-x[0:(N-1)], 2.0));
}

def rosen_der(x) {
	N = size(x);
	xm = x[1:(N-1)]
	xm_m1 = x[0:(N-2)]
	xm_p1 = x[2:N]
	der = array(double, N)
	der[1:(N-1)] = (200 * (xm - xm_m1*xm_m1) - 400 * (xm_p1 - xm*xm) * xm - 2 * (1 - xm))
	der[0] = -400 * x[0] * (x[1] - x[0]*x[0]) - 2 * (1 - x[0])
	der[N-1] = 200 * (x[N-1] - x[N-2]*x[N-2])
	return der
}

def eq_fun(x) {
	return 2*x[0] + x[1] - 1
}

def eq_jac(x) {
	return [2.0, 1.0]
}

def ieq_fun(x) {
	return [1 - x[0] - 2*x[1], 1 - x[0]*x[0] - x[1], 1 - x[0]*x[0] + x[1]]
}

def ieq_jac(x) {
	ret = matrix(DOUBLE, 2, 3)
	ret[0,:] = [-1.0, -2*x[0], -2*x[0]]
	ret[1,:] = [-2.0, -1.0, 1.0]
	return ret
}

eqCons=dict(STRING, ANY)
eqCons[`type]=`eq
eqCons[`fun]=eq_fun
eqCons[`jac]=eq_jac

ineqCons=dict(STRING, ANY)
ineqCons[`type]=`ineq
ineqCons[`fun]=ieq_fun
ineqCons[`jac]=ieq_jac

cons = [eqCons, ineqCons]

X0 = [0.5, 0]
bounds = matrix([0 -0.5, 1.0 2.0])
res = fminSLSQP(rosen, X0, rosen_der, cons, bounds, 1e-9)
res;
/* Ouput:
mode->0
xopt->[0.414944749170,0.170110501659]
fopt->0.342717574994
iterations->4
*/