Shark 计算图说明及雪球期权定价案例

1. Shark 介绍

Shark 以 DolphinDB 高效且稳定的存储系统为基础，结合 GPU 的强大算力，为用户的计算密集型分析任务提供卓越的加速能力。Shark 平台目前支持三大核心功能：GPLearn、DeviceEngine 和在 3.0.3 版本发布的 SharkGraph。其中，GPLearn 是基于 GPU 加速的因子挖掘遗传算法模块；DeviceEngine 则是专注于因子计算的 GPU 加速模块；SharkGraph 是一个通用计算模块，用于加速 DolphinDB 脚本的执行。通过这些功能，Shark 显著提升了 DolphinDB 在大规模数据分析场景下的计算效率。

2. Shark Graph 介绍

Shark Graph 支持对 DolphinDB 的函数脚本利用 GPU 进行加速。其使用方式也较为简单，只需要为需要加速的函数加上 @gpu 注解，函数的执行会自动采用 GPU 进行加速。下面是一个使用示例：

@gpu
def factory1(x) {
  sumX = sum(x)
  if (sumX  > 0) {
    return sumX
  } else {
    return avg(x) 
  }
}

factory1(1..100)

在上面的示例中，用户自定义因子计算公式 factory1，并采用 @gpu 注解。执行此函数时，DolphinDB 内部会将此函数解析为一张计算图，然后将所有参数从内存传输至 GPU 的显存，接着执行此计算图，并对自定义函数中的算子采用 GPU 进行加速，最终将结果拷贝至内存，返回给用户。

Shark Graph 目前支持的数据类型有：BOOL、CHAR、SHORT、INT、LONG、FLOAT、DOUBLE。

Shark Graph 目前支持的数据结构有：常量(Scalar)、向量(Vector)、矩阵(Matrix)、表(Table)。其中矩阵暂时不支持设置 Index，表只支持内存表。

Shark Graph 目前支持的语法是 DolphinDB 脚本语法的一个子集，包括：for 循环语句、if-else 控制语句、break、continue、赋值语句和多赋值语句。并且 Shark Graph 不支持 SQL 语法，如果用户使用 SQL 进行分析，需要改写成相对应的函数。

3. 基于 Shark Graph 的雪球期权定价案例

欧式期权的定价方法相对成熟，例如著名的 Black-Scholes 模型可以提供一个理论价格。然而，雪球期权由于其独特的结构，例如观察日和敲入敲出机制，导致其定价更为复杂，无法直接通过解析式模型得出确定的期望值。在这种情况下，数值模拟方法就显得尤为重要。其中，蒙特卡罗方法通过对标的资产价格路径的随机抽样，构建大量的模拟场景，从而估算出期权的期望价格。这种方法的一个关键特征是，模拟的次数越多，结果就越接近真实值。本节将进一步探讨如何利用 Shark Graph 优化雪球期权的蒙特卡罗模拟过程，并通过一个实际案例加以说明。

3.1 雪球期权定价算法简介

雪球期权是一种结构复杂的奇异期权，其收益结构类似于投资者卖出的一种带有触发条件的看跌期权。雪球期权的核心在于其“障碍”条款，即预设的标的资产价格触发水平。“障碍”的设置使得期权只有在标的价格触及特定水平时才会发生结构性变化。一般而言，“障碍”分为“敲出”和“敲入”两种类型。“敲出障碍”规定了当标的资产价格达到预设的“敲出水平”时，期权提前终止并进行结算；若未触及，则期权按原定条款运行。“敲入障碍”则规定了只有当标的资产价格达到“敲入水平”时，期权才会触发约定的收益结构；若未触及，则该收益结构可能不会生效。

下面将会给出一个雪球期权定价的案例，图 1 展示了本案例流程。

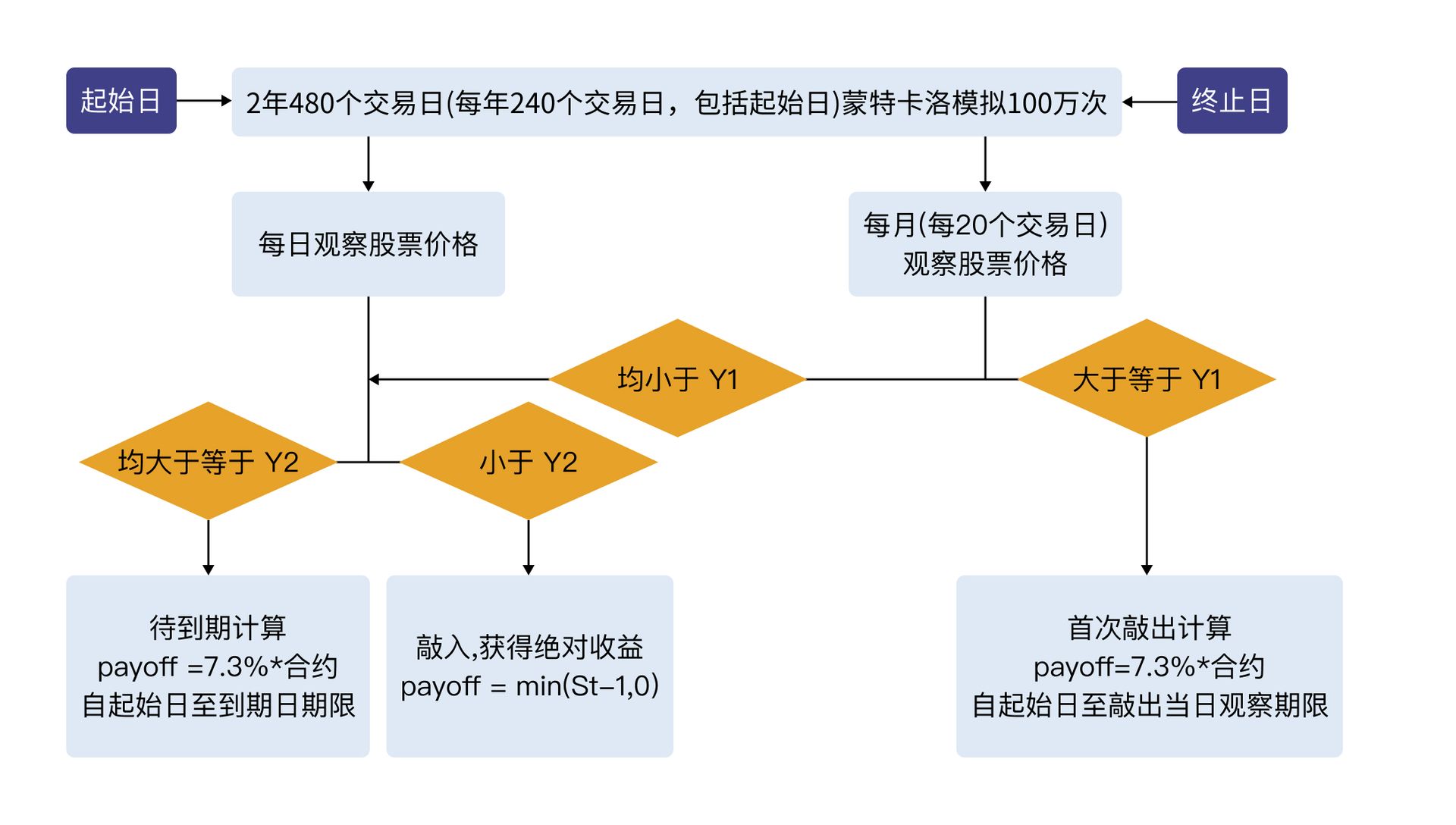
计算流程如下所示：

假设每年 240 个交易日，包括起始日一共 480 个交易日，蒙特卡洛模拟 100 万次。先生成 size 为1000000*480 符合标准正态分布的随机数矩阵 z。
假设股票初始价格 S0 为 1，波动率 vol 为 13%，无风险利率 r 为 3%，股息率 q 为 8%，利用步骤 1 中随机数矩阵 z 生成符合几何布朗运动的股票价格矩阵。首先初始化起初价格 s(：,1)=S0，然后s(：,i+1) = s(：,i) * exp((r-q-vol^2/2)*(1/240)+vol*sqrt(1/240)*z(：,i))。
对 100 万次模拟路径中每次模拟的路径，每日观察是否敲入（股票价格低于 Y2，即 0.7），每月（每 20 个交易日）观察是否敲出（股票价格高于 Y1，即 1）。因此，基于雪球期权的规则，共有三种情形：
1. 如果在每月的观察日期敲出，则客户赚得 payoff=7.3%* 合约，自起始日至敲出当日观察期限。
2. 合约 24 个月后始终未敲出则自然到期，如果期间未敲入，则客户赚得 payoff=7.3%* 合约自起始日至到期日期限。
3. 合约 24 个月后始终未敲出则自然到期，但期间发生了敲入，则最终兑付收益为 payoff=min(S_T-1,0)（S_T 代表该模拟路径最后价格）。
完成 100 万次模拟，并且记录这 100 万次模拟的状态、持有期限以及收益。之后，对这 100 万次路径折现后的最终收益求平均值，即为雪球期权最终的定价 price。
完成以上定价函数后，为了确保当前计算出来的价格的准确性，使用有限差分公式计算期权的 Greeks 值，包括 Delta, Gamma, Theta, Vega, Rho。设置 ΔS 为 0.005，例如计算 Delta 的公式为：，即分别计算标的价格为 S₀± ΔS 的雪球期权定价，在此例中，仍采用蒙卡模拟法，因此仍需要重新模拟并获得对应的期权价格。

完整的计算流程代码详见附录。

3.2 利用 Shark Graph 加速雪球期权定价算法

在附录 1 的案例中，DolphinDB 脚本使用了 ploop 函数，将单线程循环转换成多线程并行计算，之后将结果进行拼接以提升效率。但是在 Shark Graph 中，用户无需关心这些细节，Shark 会自动使用 GPU 并行化算子的计算。利用 Shark Graph 计算雪球期权定价的脚本详见附录 2。

下面测试了利用 Shark Graph 和 DolphinDB 并行编程计算雪球定价的性能，其中测试环境为


软硬件项	信息
OS（操作系统）	CentOS Linux 7 (Core)
内核	3.10.0-1160.el7.x86_64
CPU 类型	AMD EPYC 7513 32-Core Processor
CPU 逻辑核数	128 core
内存	512 GB
GPU	NVIDIA A800 80GB PCIe

本案例测试了 DolphinDB 不同并发度和不同蒙特卡洛模拟迭代次数下，利用 CPU 计算和 GPU 计算之间的耗时（单位：毫秒 ms），测试结果如下表所述：


迭代次数		1 千次	1 万次	10 万次	100 万次
DolphinDB 并发数	8	40.49	406.04	2504.10	26546.84
	16	13.21	244.60	1464.68	14306.35
	32	12.47	129.80	1053.39	9908.71
	64	11.61	99.57	779.49	7742.04
	128	27.38	63.39	577.26	6213.23
Shark Graph		2.87	6.20	40.90	372.36

加速比如下图所示：

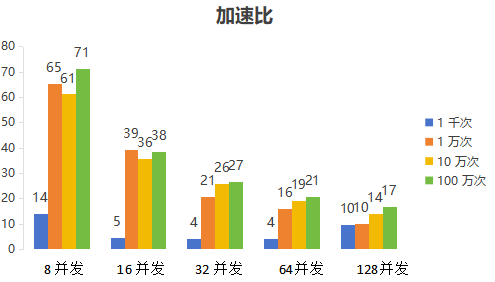
在大规模迭代场景下，Shark 相比 DolphinDB 的并发具有显著优势。相比 DolphinDB 8 个并发度，Shark 可以达到最高 70 倍的提速；即使中等规模的迭代，也可以达到 61 倍的提速。相较于单块 CPU ( 32 core, 64 thread)，单块 NVIDIA A800 GPU 虽价格高出 9-10 倍，但在 DolphinDB 64 并发下，Shark 的性能优势仍高达 20 倍。

因此对于计算密集型的任务，Shark 的 GPU 加速提供了更具竞争力的性价比。

4. 结语

本文介绍了一种使用 DolphinDB 异构计算平台 Shark 加速 DolphinDB 计算脚本的解决方案，用户只需要为计算函数添加 @gpu 注解，就可以直接使用 GPU 加速脚本。在利用 Shark 加速雪球计算脚本的案例中，Shark 相比 CPU 并发执行的方式，最高达到了 65 倍的加速比，即使对于中等规模的蒙特卡洛模拟，也可以达到 57 倍的加速比。

5. 附录

附录 1 DolphinDB 雪球定价代码

//%模拟次数参数
N = 1000000;

//%底层资产参数
vol   = 0.13;
S0    = 1;
r     = 0.03;
q     = 0.08;

//%日期参数
days_in_year = 240; //一年交易日
dt    = 1\days_in_year; //每日

//%障碍期权（雪球内嵌）参数
T     = 2; //期限，按年份
Tdays = T * days_in_year; //期限，按交易日
Y1    = 1*S0;   //敲出价
Y2    = 0.8*S0; //敲入价
observation_idx = 20+20*(0..(Tdays/20-1)) //观察日，只在此观察日观察是否敲出
all_t = dt +dt*(0..(T*days_in_year-1))

St = 1;

//%目标利润率
profit = 0.003*S0;

con_level = 100

def coupon(N,vol,S0,r,q,T,Y1,Y2,observation_idx,St,profit,num){

	days_in_year = 240; //一年交易日
	dt    = 1\days_in_year; //每日
	all_t = dt +dt*(0..int(T*days_in_year-1))
	Tdays =int(T * days_in_year); //期限，按交易日

	S = St * exp((r - q - vol*vol/2) * repmat(matrix(all_t),1,N) + vol * sqrt(dt) * cumsum(norm(0,1,Tdays*N)$Tdays:N))

	//status
	knockout_matrix = S[observation_idx-1,0..(N-1)]>Y1
	status =iif(sum(S[observation_idx-1,0..(N-1)]>Y1)>0,1,iif(sum(S<Y2)==0,-1,0))

	//t_holding
	k= observation_idx*(S[observation_idx-1,0..(N-1)]>Y1)
	kk=iif(k==0,NULL,k)
	kkk = bfill(kk)
	res = kkk[0,].flatten()
	t_holding =all_t[res].nullFill!(double(T))

	//pay_off
	tmp_nag = min(0, last(S)/S0-1)
	payoff = iif(status*t_holding>0,status*t_holding,iif(status*t_holding==0,double(T),tmp_nag))
	res = table(status,t_holding,payoff)
	return res
}

def barrier_coupon(N,vol,S0,r,q,T,Y1,Y2,observation_idx,St,profit,con_level){
	con = int(N\con_level)
	nloop =1..(con_level)
	a = ploop(coupon{con,vol,S0,r,q,T,Y1,Y2,observation_idx,St,profit},nloop).unionAll(false)

	if (- profit*N - (exec sum(exp(-r * t_holding) * payoff) from a where status = -1) > 0){
	   	C   = (- profit*N - (exec sum(exp(-r * t_holding) * payoff) from a where status = -1)) /(exec sum(exp(-r * t_holding) * payoff) from a where status != -1)
	   	return C
	}else{
		C = 0
	    	return C
	} 
}

def pricing(N,vol,S0,r,q,T,Y1,Y2,observation_idx,St,profit,C,num){
	//%日期参数
	days_in_year = 240; //一年交易日
	dt    = 1\days_in_year; //每日
	all_t = dt +dt*(0..int(T*days_in_year-1))
	Tdays = int(T * days_in_year); //期限，按交易日
	
	S = St * exp( (r - q - vol*vol/2) * repmat(matrix(all_t),1,N) + vol * sqrt(dt) * cumsum(norm(0,1,Tdays*N)$Tdays:N))

	//status
	knockout_matrix = S[observation_idx-1,0..(N-1)]>Y1
	status =iif(sum(S[observation_idx-1,0..(N-1)]>Y1)>0,1,iif(sum(S<Y2)==0,-1,0))

	//t_holding
	k= observation_idx*(S[observation_idx-1,0..(N-1)]>Y1)
	kk=iif(k==0,NULL,k)
	kkk = bfill(kk)
	res = kkk[0,].flatten()
	t_holding =all_t[res].nullFill!(double(T))

	//pay_off
	tmp_nag = min(0, last(S)/S0-1)
	payoff = iif(status*t_holding>0,C*status*t_holding,iif(status*t_holding==0,C*double(T),tmp_nag))
	res = table(status,t_holding,payoff)
	return res
}


def barrier_pricing(N,vol,S0,r,q,T,Y1,Y2,observation_idx,St,profit,C,con_level){
	con = int(N\con_level)
	nloop =1..(con_level)
	a = ploop(pricing{con,vol,S0,r,q,T,Y1,Y2,observation_idx,St,profit,C},nloop).unionAll(false)

	price = mean(exp(-r*a.t_holding) *a.payoff)
	return price
}


timer C = round(barrier_coupon(N,vol,S0,r,q,T,Y1,Y2,observation_idx,St,profit*S0,con_level),3)


if (C>0){
	timer     price_St_plus = barrier_pricing(N,vol,S0,r,q,T,Y1,Y2,observation_idx,St*(1 + 0.005),profit,C,con_level);
	timer     price_St_minus = barrier_pricing(N,vol,S0,r,q,T,Y1,Y2,observation_idx,St*(1 - 0.005),profit,C,con_level);
	timer     price_vol_plus = barrier_pricing(N,vol + 0.01,S0,r,q,T,Y1,Y2,observation_idx,St,profit,C,con_level);
	timer     price_vol_minus = barrier_pricing(N,vol - 0.01,S0,r,q,T,Y1,Y2,observation_idx,St,profit,C,con_level);
	timer     price_after_oneday = barrier_pricing(N,vol,S0,r,q,T - dt,Y1,Y2,observation_idx-1,St,profit,C,con_level);
	    
	timer     price = barrier_pricing(N,vol,S0,r,q,T,Y1,Y2,observation_idx,St,profit,C,con_level);
	timer     delta = (price_St_plus - price_St_minus)/2/St/(St*0.005);
	timer     gamma = (price_St_plus - 2*price + price_St_minus)/St/St/(St*0.005)/(St*0.005);
	timer     vega  = (price_vol_plus - price_vol_minus)/2/0.01;
	timer     theta = (price - price_after_oneday)/dt;
}
else{
	price = NULL
	delta =  NULL
	gamma =  NULL
	vega  =  NULL
	theta =  NULL
}

附录 2 Shark 计算雪球定价

 

//%模拟次数参数
N = 1000000;

//%底层资产参数
vol   = 0.13;
S0    = 1;
r     = 0.03;
q     = 0.08;

//%日期参数
days_in_year = 240; //一年交易日
dt    = 1\days_in_year; //每日

//%障碍期权（雪球内嵌）参数
T     = 2; //期限，按年份
Tdays = T * days_in_year; //期限，按交易日
Y1    = 1*S0;   //敲出价
Y2    = 0.8*S0; //敲入价
observation_idx = 20+20*(0..(Tdays/20-1)) //观察日，只在此观察日观察是否敲出
all_t = dt +dt*(0..(T*days_in_year-1))

St = 1;

//%目标利润率
profit = 0.003*S0;

con_level = 100

def coupon(N,vol,S0,r,q,T,Y1,Y2,observation_idx,St,profit){
 
    days_in_year = 240; //一年交易日
    dt    = 1\days_in_year; //每日
    all_t = dt +dt*(0..int(T*days_in_year-1))
    Tdays =int(T * days_in_year); //期限，按交易日
    S = St * exp((r - q - vol*vol/2) * repmat(matrix(all_t),1,N) + vol * sqrt(dt) * cumsum(norm(0,1,Tdays*N)$Tdays:N))

    //status
    knockout_matrix = S[observation_idx-1,0..(N-1)]>Y1
    status =iif(sum(knockout_matrix)>0,1,iif(sum(S<Y2)==0,-1,0))

    //t_holding
    k= observation_idx*(knockout_matrix)
    kk=iif(k==0,NULL,k)
    kkk = bfill(kk)
    res = kkk[0,].flatten()
    t_holding =all_t[res].nullFill(double(T))

    //pay_off
    statusxtholdings = status*t_holding
    tmp_nag = min(0, last(S)/S0-1)
    payoff = iif(statusxtholdings>0,statusxtholdings,iif(statusxtholdings==0,double(T),tmp_nag))
    res = table(status,t_holding,payoff)

    index = res.status == -1
    aut = res.payoff[index]
    sum1 = sum(exp(-r * res.t_holding[index]) * res.payoff[index])

    if (- profit*N - sum1 > 0){
        index2 = res.status != -1
        sum2 = sum(exp(-r * res.t_holding[index2]) * res.payoff[index2])
        C = (- profit*N - sum1 ) / sum2
        return C
    }else{
        return  0
    }
}

// fn = createSharkGraph(snowRun)
// fn.genGraphDotFile("/home/jpma/testDB/release300.graph/build/dos/1.dot")
// fn.dumpGraphCode("/home/jpma/testDB/release300.graph/build/dos/D20-20840.rewrite.dos")

def pricing(N,vol,S0,r,q,T,Y1,Y2,observation_idx,St,profit,C,num){
    //%日期参数
    days_in_year = 240; //一年交易日
    dt    = 1\days_in_year; //每日
    all_t = dt +dt*(0..int(T*days_in_year-1))
    Tdays = int(T * days_in_year); //期限，按交易日
    
    S = St * exp( (r - q - vol*vol/2) * repmat(matrix(all_t),1,N) + vol * sqrt(dt) * cumsum(norm(0,1,Tdays*N)$Tdays:N))

    //status
    knockout_matrix = S[observation_idx-1,0..(N-1)]>Y1
    status =iif(sum(knockout_matrix)>0,1,iif(sum(S<Y2)==0,-1,0))

    //t_holding
    k= observation_idx*(knockout_matrix)
    kk=iif(k==0,NULL,k)
    kkk = bfill(kk)
    res = kkk[0,].flatten()
    t_holding =all_t[res].nullFill(double(T))

    // pay_off
    statusxtholdings = status*t_holding
    tmp_nag = min(0, last(S)/S0-1)
    payoff = iif(statusxtholdings>0,C*statusxtholdings,iif(statusxtholdings==0,C*double(T),tmp_nag))
    res = table(status,t_holding,payoff)
    return res
}

def barrier_pricing(N,vol,S0,r,q,T,Y1,Y2,observation_idx,St,profit,C){
    res= pricing(N,vol,S0,r,q,T,Y1,Y2,observation_idx,St,profit,C, 1)
    return mean(exp(-r*res.t_holding) *res.payoff)
}


@gpu
def snowRun(N, vol, S0, r, q, T, Y1, Y2, observation_idx, St, profit, con_level, dt) {
    C = round(coupon(N, vol, S0, r, q, T, Y1, Y2, observation_idx, St, profit * S0), 3) 
    if (C > 0) {
        price_St_plus =
            barrier_pricing(N, vol, S0, r, q, T, Y1, Y2, observation_idx, St * (1 + 0.005), profit, C);
        price_St_minus =
            barrier_pricing(N, vol, S0, r, q, T, Y1, Y2, observation_idx, St * (1 - 0.005), profit, C);
        price_vol_plus = barrier_pricing(N, vol + 0.01, S0, r, q, T, Y1, Y2, observation_idx, St, profit, C);
        price_vol_minus =
            barrier_pricing(N, vol - 0.01, S0, r, q, T, Y1, Y2, observation_idx, St, profit, C);
        price_after_oneday =
            barrier_pricing(N, vol, S0, r, q, T - dt, Y1, Y2, observation_idx - 1, St, profit, C);

        price = barrier_pricing(N, vol, S0, r, q, T, Y1, Y2, observation_idx, St, profit, C);
        delta = (price_St_plus - price_St_minus) / 2 / St / (St * 0.005);
        gamma = (price_St_plus - 2 * price + price_St_minus) / St / St / (St * 0.005) / (St * 0.005);
        vega = (price_vol_plus - price_vol_minus) / 2 / 0.01;
        theta = (price - price_after_oneday) / dt;
    }
    else {
        price = 1
        delta = NULL
        gamma = NULL
        vega = NULL
        theta = NULL
    }
    return price
}


timer {
     a1 = snowRun(N, vol, S0, r, q, T, Y1, Y2, observation_idx, St, profit, con_level, dt) 
}