基于 DolphinDB 的因子归因分析
在金融市场中,任何一只股票在同一时点都暴露于多种不同的因素之下,它们之间的共同作用形成了股票价格的波动。随着量化方法与大数据技术的广泛应用,越来越多的投资者采用多因子模型来解释和预测股票收益。这些因子通常包括风格因子(如动量、价值、波动率、规模等)、行业因子和特定因子,能够从不同维度揭示股票价格的系统性变化来源。
因子归因分析,正是通过将投资组合相对于基准的超额收益与主动风险系统性地拆解到各类风险因子上,以识别和量化不同因子对组合表现的具体贡献。这种分析不仅有助于评估投资组合的历史绩效,还能为未来的投资优化与风险控制提供重要参考。因子归因的整体流程可分为三个部分:纯因子收益估计、主动收益归因、主动风险归因。本文将基于 DolphinDB 语言以及因子归因模型,介绍因子归因模块以便用户进行分析。
1. 模型介绍
多因子模型是一种用于解释和预测股票收益的金融模型,它认为股票组合的收益可以由多个因子共同决定。我们先来简单介绍一下 Barra CNE5+ 中的多因子模型。假设 N 支股票组合,考虑任意一支股票 j,其超额收益率由 K 个因子线性分解,包含 p 个行业因子和 q 个风格因子 。一般表达式如下:
其中 rj 为个股 j 的超额收益率,Xi 代表着因子 i 的暴露度向量,fi 为因子 i 的因子收益率向量, μⱼ 为个股 j 的主动残差值。记 X = [X1,X2,…,XK] 为因子暴露矩阵,r = [r₁, r₂, ..., rN] 为 N 支股票组合 T 日的超额收益率向量 。
-
因子暴露矩阵 X 由行业因子哑变量矩阵和风险因子暴露矩阵构成,其中行业因子哑变量矩阵根据股票的行业所属生成,风险因子暴露矩阵由 T 日的股票历史数据所得。
纯因子收益率 fi 由纯因子组合权重 ωi 与股票超额收益率向量 r 得到,如下:
下面我们将介绍因子归因的三个主要步骤:包括纯因子收益估计、主动收益归因、主动风险归因。
1.1 纯因子收益估计
纯因子股票组合体现的是,股票投资组合只暴露于某一个特定因子,而对其他因子以及行业因子影响保持中性,从而更好地分析因子本身的真实收益和风险特征。因此,我们需要在行业中性以及风格因子中性的约束下,估计各个风格因子的纯因子组合权重。行业中性体现为股票组合的行业配置与基准的行业配置保持一致,而风格中性体现为股票组合的风格因子较之基准的风险暴露为 0。
基于上述纯因子股票组合的背景,考虑第 j 个风格因子,线性规划问题如下:
目标函数: ω 为第 j 个风格因子的权重向量, Xj 为第 j 个风格因子的暴露向量。本模块中考虑最大化目标因子暴露度,其他常见的目标函数有最大化投资组合夏普率,最小化投资组合风险等等。
约束条件:第一条是风格中性约束条件,保证了对其余风格因子的暴露为 0 ;第二条是行业中性约束条件,H 代表着股票的行业因子哑变量矩阵,h 代表着基准对应的行业权重向量;由于 A 股无法做空,因此需要限制任一股票的权重系数不为负。
值得注意的是,上面的约束条件仅能满足对其余风格因子暴露为 0 个单位,而对指定因子的暴露并没有严格约束为 1 个单位。本模块中添加了以下约束:
因此,基于行业中性与风格中性的约束下,构造对不同风格因子 j 完全暴露的纯因子组合权重 ωj,并与 T 日的股票超额收益率向量 r 结合得到纯因子收益率:
1.2 主动收益归因
主动收益归因是指将股票组合的超额收益(组合收益-基准收益)系统性地分解到各类因子上,有助于投资者明确超额收益的来源、因子的有效性和合理性。由于构造纯因子组合时将行业因子中性化处理,因此只对 q 个风格因子进行归因分析。因子主动收益归因模型如下:
记股票组合和基准权重分别为 ωP, ωb ,得到超额权重 ωA = ωP - ωb。根据风格因子暴露矩阵 X 以及超额收益率向量 r ,计算得到因子主动暴露度 XA = ωA·X,超额收益值 rA = ωA·r 。再结合 1.1 节中求得的纯因子收益向量 f=[f1,f2,⋯,fq],可对股票组合的超额收益进行如下的分解:
因子贡献 = XAf
残差:
1.3 主动风险归因
主动风险归因是指将股票组合较于基准的风险分解到各类因子上,有助于投资者识别是否存在过度集中、过度偏离某因子的风险、更好地控制投资决策中的风险来源。基于MSCI Barra 提出的 X-Sigma-Rho 归因模型,因子主动风险归因表达式为:
其中 XA 为因子主动暴露度,σ 为波动率方差,ρ 为相关性。由上式可以看出,股票组合收益 rA 的主动风险归因于因子主动暴露度,因子收益的波动率以及相关性。因子主动暴露度反映了组合的风格倾向,是主动风险的主要来源;因子收益波动率反映了组合无法控制的被动风险来源;而相关性部分反映了股票组合收益与因子之间的联动关系。
2. 模块使用方法
2.1 数据预处理
首先,用户需要对因子归因的相关数据表进行处理,保证各表的字段与下列示例一致。若用户无相关数据表,可以参考附件 2 模拟数据生成。部分模拟数据示例如下:
- bench 市场基准信息:每日个股的基准权重。
- own 持仓权重表:每日个股的持仓权重。
- market 股票收益表:每日个股的收益率。
- styleExpos 风格因子暴露表:每日个股的风格因子暴露表。

- industryExpos 行业因子暴露表:每日个股所属的行业因子哑变量表。
2.2 参数设置
除了上述因子归因的相关数据表之外,用户还需设置 startDate,endDate 来规定归因分析日期。若需对风格因子暴露表进行标准化,则设定 standard = true。
2.3 函数调用
使用 getHomeDir() 获取主目录,并将附件
1 模块文件放入对应的模块路径。用户需要使用 use 导入因子归因模块:
use factorAttributionUtils
go在设置好相关参数之后,调用函数即可获取归因结果:纯因子收益率表 purefactorTb、因子贡献残差表 factorAttResTb,主动风险归因表 riskTb。
attriResultDict = attributionFunc(startDate, endDate, bench, own, market, styleExpos,
industryExpos, windowSize, standard=false)2.4 查看结果
通过指定 attriResultDict 的键值(纯因子收益率/主动收益归因/主动风险归因)获取对应的归因表,例如
attriResultDict[`纯因子收益率]。模拟数据的结果如下:



注意:如需绘图查看,可指定需查看的结果类型 resType 以及日期 targetDate:
resType = "纯因子收益率" //指定"纯因子收益率" 或者 `主动收益归因 或者 `主动风险归因
resTb = attriResultDict[resType]
factorCols = columnNames(resTb)[1:]
plot(resTb[factorCols], resTb[`date], resType)
//若要查看某一日的因子归因结果,需指定targetDate
targetDate = 2023.10.01
sliceData = select * from resTb where date = targetDate
factorValues = flatten(matrix(sliceData[factorCols]))
plot(factorValues, factorCols, resType+" - " + string(targetDate), COLUMN)对模拟数据的结果进行绘制,部分因子归因的结果曲线示例如下:
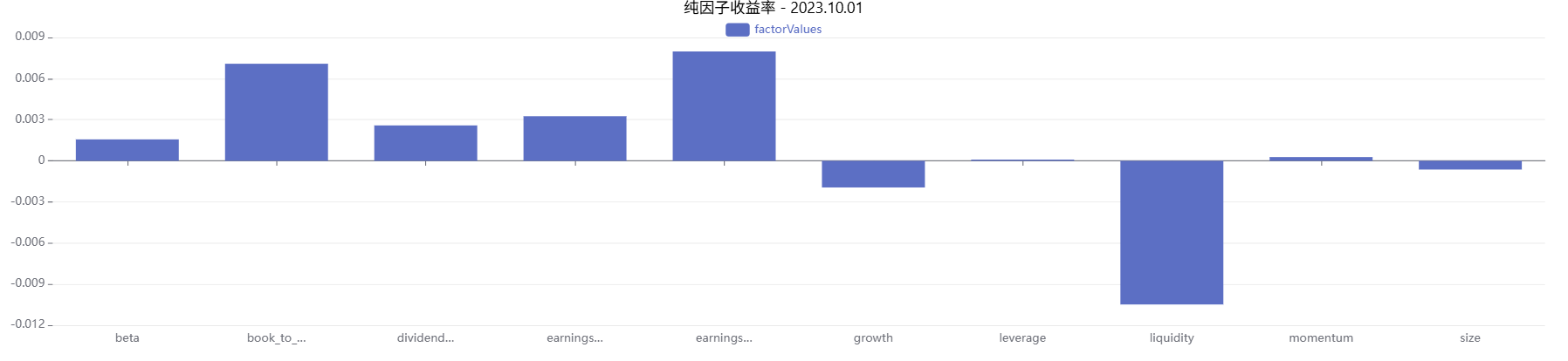
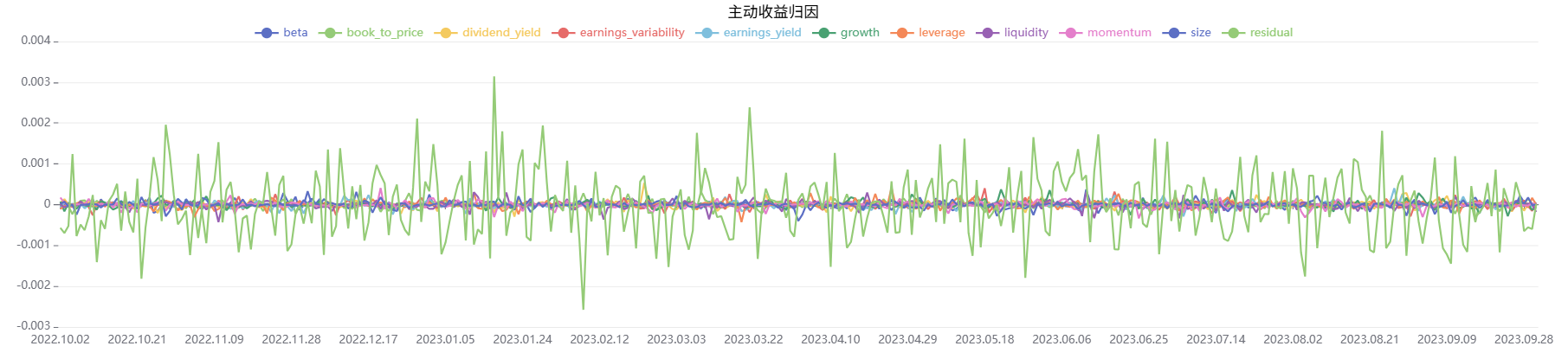
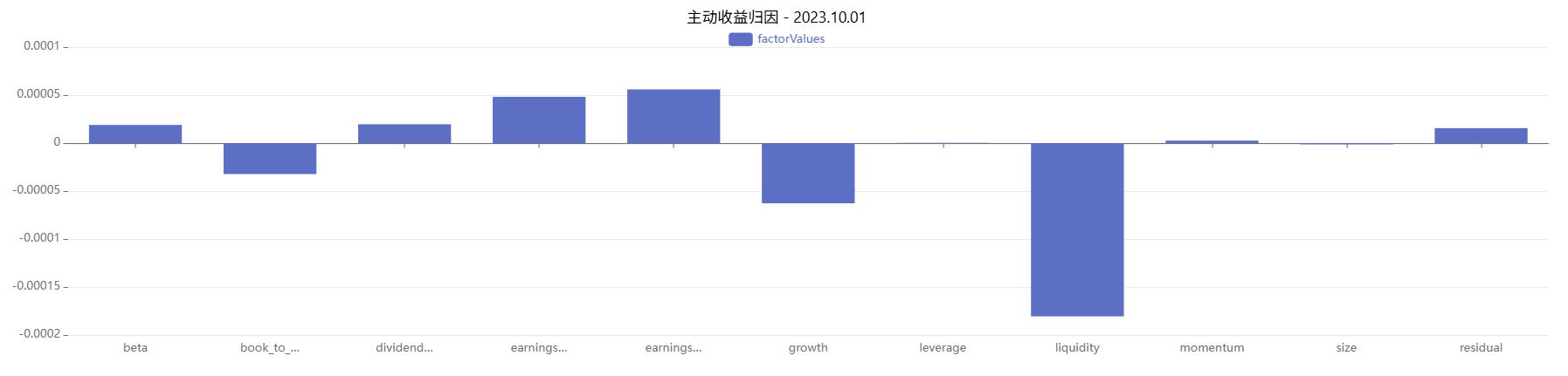
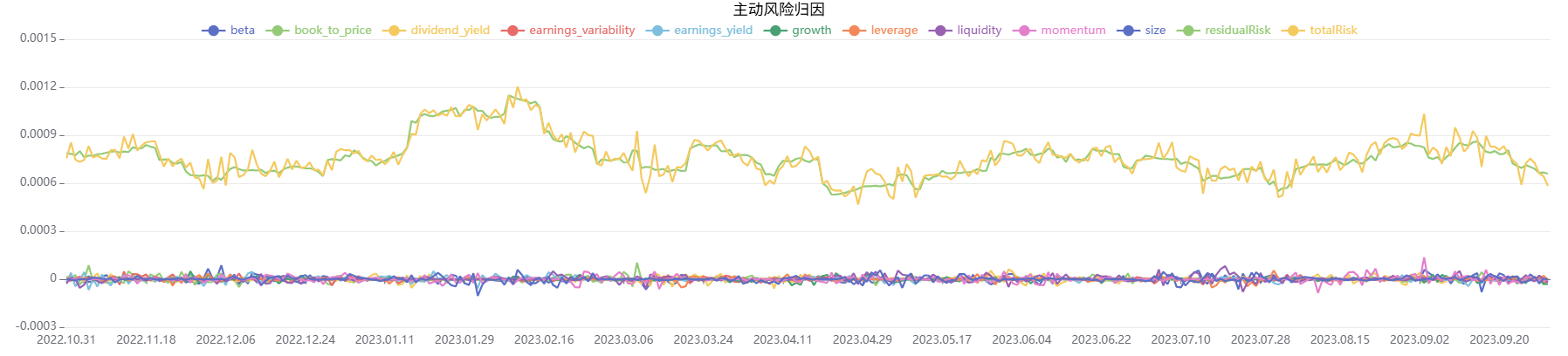
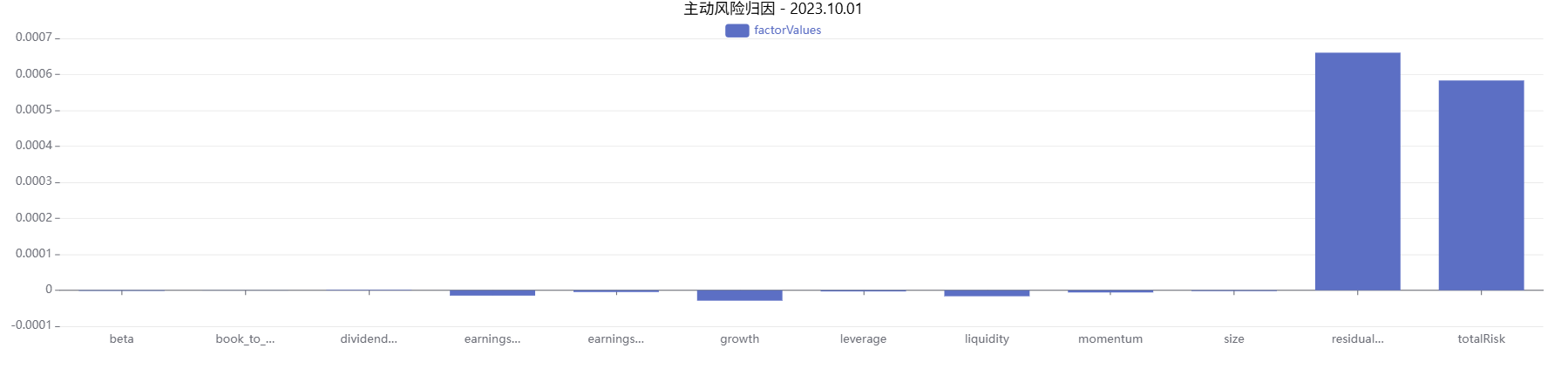
3. 函数计算性能
该因子归因模块中的函数均通过 DolphinDB 的内置函数 peach、each
对不同交易日以及不同的风格因子,实现了并发计算处理,提升了因子归因的计算效率。 本节将具体展示基于 DolphinDB 实现的归因函数
attributionFunc 的计算性能。通过在不同日期范围 startDate,endDate 以及
widowSize 设置下的性能测试,帮助用户更好地理解该模块函数的计算复杂度、以及在实际应用中的表现。
3.1 测试方法
模拟数据:
- 基准数据 (bench):模拟了 10 年期间每日的基准持仓信息。
- 持仓权重数据 (own):模拟了 10 年期间每日的持仓权重信息。
- 收益数据 (market):模拟了 10 年期间 1000 只股票的收益数据。
- 风格因子暴露 (styleExpos):模拟了 10 年内 10 个风格因子的暴露信息。
- 行业因子暴露 (industryExpos):模拟了10 年内 30 个行业因子的暴露信息。
3.2 测试结果
设置不同的回测时长、风格因子个数分别进行测试,按日频调仓得到归因函数的耗时如下:
| 回测时间 | 风格因子个数 | 耗时 |
|---|---|---|
| 10 年 | 20 | 1 min 43 s |
| 5 年 | 20 | 48 s |
| 1 年 | 20 | 11 s |
| 10 年 | 10 | 32 s |
| 5 年 | 10 | 17s |
| 1 年 | 10 | 3s |
4. 总结
本文基于 DolphinDB 内置的统计分析函数库、高效的并行计算、便捷的表连接方式以及向量化编程特性,根据因子归因模型开发实现了归因模块。将 DolphinDB 自身强大的计算功能与因子归因模型结合,能帮助用户更高效更精准地进行归因分析,了解投资组合超额收益与风险的组成来源,是投资决策的不可或缺的一部分。
5. 附件
- 模块文件:factorAttributionUtils.dos
- 模块测试文件:factorTestScript.dos
- 函数具体说明:因子归因模块参数说明.pdf
