CPU-GPU 异构计算平台 Shark 应用:蒙特卡罗模拟定价
近年来,随着摩尔定律逐渐逼近极限,处理器单核性能的提升速度显著放缓。与此同时,大数据与人工智能技术的迅速发展带来了计算需求的爆炸式增长。为应对这一挑战,采用 GPU 、FPGA 等处理器来加速计算已成为重要的技术方向。本文将主要介绍 DolphinDB CPU-GPU 异构计算平台 Shark 加速脚本计算的解决方案,并在 FICC 领域的雪球期权定价、票息率确定的应用场景中展示 Shark 的强大计算性能。
1. Shark 介绍
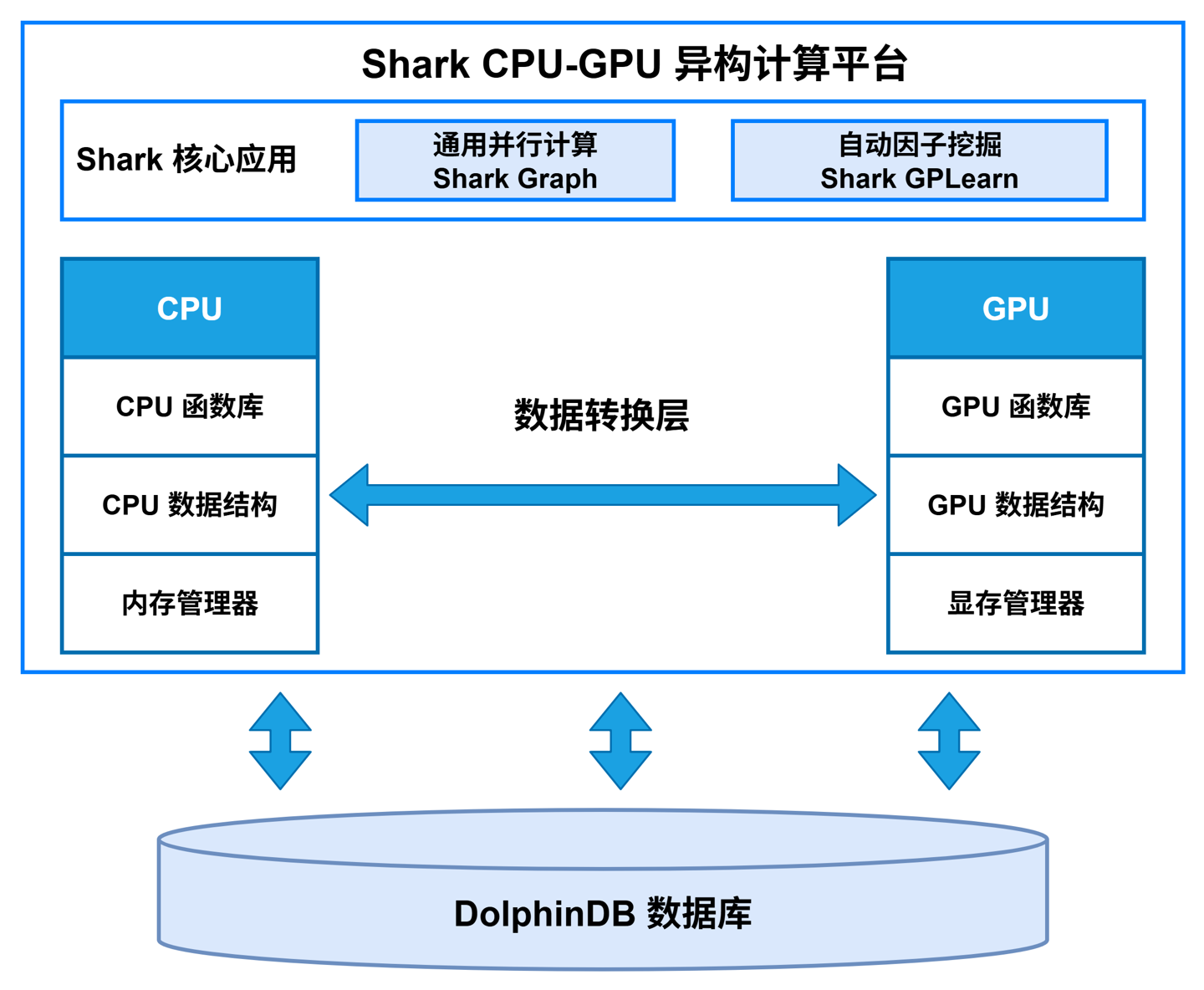
Shark 是 DolphinDB 3.0 推出的 CPU-GPU 异构计算平台。它以 DolphinDB 的高效存储系统为底层支撑,深度融合 GPU 并行算力,能够为计算密集型任务提供显著的性能加速。Shark 平台基于 CPU-GPU 异构计算框架,提供两大核心功能:
- Shark Graph:通过 GPU 加速 DolphinDB 的通用计算脚本,实现复杂分析任务的并行化执行。
- Shark GPLearn:专为因子挖掘场景设计,支持基于遗传算法的自动化因子发现与优化。
通过这些功能,Shark 能够帮助 DolphinDB 突破 CPU 算力瓶颈,显著提升 DolphinDB 在高频量化、实时风控等大规模数据分析场景下的计算效率。
1.1 Shark 计算平台架构
Shark 计算平台的数据转换层负责内存与显存之间的数据交互。在计算开始的时候,数据转换层通过 CPU 把数据从磁盘读取到内存,再将内存中的数据复制至 GPU 的显存,以供后续 GPU 上的计算使用。当 GPU 上的计算完成后,数据转换层将显存中的数据复制到内存,最后通过 CPU 将其存储至 DolphinDB 数据库中。
Shark 计算平台构建了 GPU 上的基础数据结构,包括向量、矩阵、表等。在这些数据结构的基础上,Shark 的 GPU 函数库将支持 DolphinDB 原本 CPU 上已经支持的丰富函数库,从而能够利用 DolphinDB 的脚本语言调用 GPU 进行多种复杂运算。此外,为了优化计算任务中显存的分配和释放管理,Shark 自研了 GPU 的显存管理器。
1.2 数据传输模块
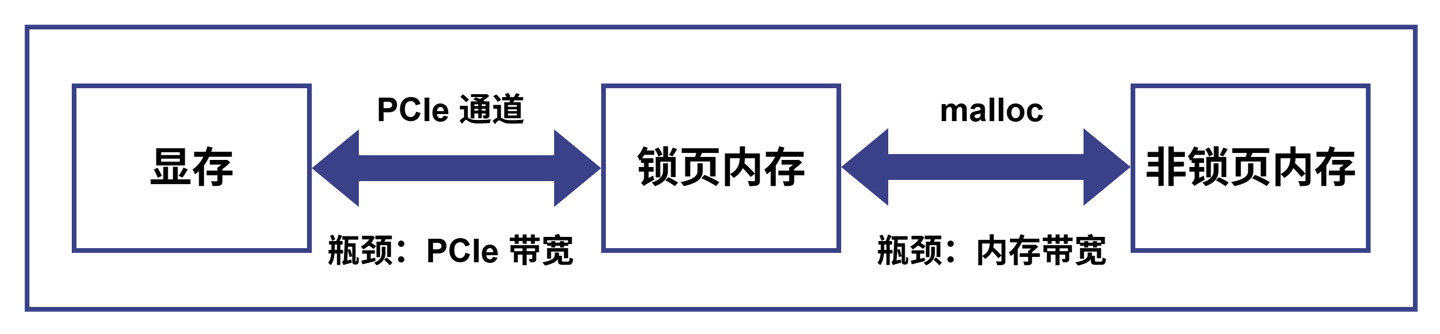
数据传输模块是 Shark 中负责 CPU 和 GPU 通信的桥梁,Shark 架构中上层应用的所有数据交互和传输均由这个模块完成。对于复杂的数据分析任务而言,显存和内存的数据传输效率是整个任务流的瓶颈所在。以显存的数据拷贝到内存为例,传输过程分为两阶段。首先,数据从常规内存,也就是通过 malloc 分配的非锁页内存,迁移到锁页内存,这一阶段的传输速率取决于内存带宽。接着,数据需通过 PCIe 通道从锁页内存传输至显存,此时传输速率则由 PCIe 带宽决定。这两个阶段的耗时叠加,就构成了整个通信过程的时间成本。
在实时高频因子计算的场景中,由于每次传输的数据量非常小,GPU 并行计算耗时非常短,实际测试发现将近 90% 的时间消耗在基础数据传输过程中。当 GPU 计算单元每秒能处理百万级任务时,这种因通信延迟导致的算力闲置,实质上造成了巨大的隐性成本。由于拷贝流程是一个多阶段任务,每个阶段完成后才能进入下一个阶段,因此考虑使用一个经典的计算机优化思想—— PipeLine 流水线化。

Shark 首先将数据按 2MB 为一个块进行划分,然后采用多线程分块拷贝的方式,每个线程负责多个数据块。在单个线程内部,数据会先从显存拷贝到锁页内存,再从锁页内存拷贝到非锁页内存。通过这种流水线式的处理方式,Shark 在牺牲一定 PCIe 带宽的情况下,大幅提升了内存带宽的利用效率。
2. Shark Graph
本文的应用案例主要是通过 Shark Graph 功能来实现 GPU 加速计算的,所以此处对 Shark Graph 进行详细介绍。读者如果对 Shark GPLearn 因子自动挖掘功能感兴趣,可以查看相关应用教程。
2.1 功能介绍
在金融领域中,由许多业务场景充满了计算密集型任务,如量化交易的因子计算、 FICC 领域的雪球期权定价、票息率确定和多维蒙卡计算等。这些场景非常适合通过 GPU
的并行计算能力加速计算。因此,Shark 推出了 Shark Graph 功能。用户无需修改自己的 DolphinDB 脚本(CPU
执行的计算代码),只需要加上 @gpu 注解,Shark 就会自动在 GPU 上编排调度脚本计算任务,并且利用 GPU
加速计算。在这种使用方式下,研究员无需使用 CUDA 改写 DolphinDB 脚本,且在已经有存量 DolphinDB
脚本的情况下,可以非常便捷地把计算任务调度到 GPU 上运行。
Shark Graph 目前支持的数据类型有:BOOL、CHAR、SHORT、INT、LONG、FLOAT、DOUBLE。
Shark Graph 目前支持的数据结构有:常量(Scalar)、向量(Vector)、矩阵(Matrix)、表(Table)。其中矩阵暂时不支持设置Index,表只支持内存表。
Shark Graph 目前支持的语法是 DolphinDB 脚本语法的一个子集,包括:for 循环语句、if-else控制语句、break、continue、赋值语句和多赋值语句。Shark Graph 目前不支持 SQL 语法,若要使用SQL进行分析,需要改写成相对应的函数。
Shark Graph 具有以下优点:
- 学习成本低:用户只需要采用添加注解的方式,就可以直接使用 DolphinDB 脚本在 GPU 上加速计算。
- 迁移成本低:Shark Graph 完全兼容 DolphinDB 脚本的执行方式和数据结构,已有存量 DolphinDB 脚本稍作改造即可把计算任务调度到 GPU 上运行。
- 计算效率高:对于一些计算密集型的金融计算任务,如本文中提到的蒙特卡洛雪球期权定价场景,相对Python 可以达到 200 倍的加速比。
2.2 工作流程
对于用户自定义的函数脚本,Shark Graph 首先将其解析并转换为一个有向无环图,例如下图所示的函数:
@gpu
def factor(a, b){
sumA = sum(a)
sumB = sum(b)
return sumA + sumB + corr(a, b)
}将会被转化为这样的计算图:
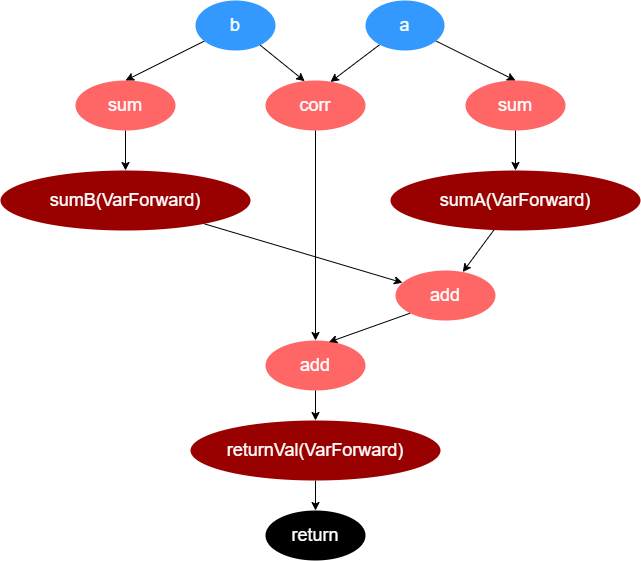
然后 Shark Graph 会对计算图进行广度优先遍历(BFS),将图中的节点放入工作队列。每次从工作队列中取出一个节点执行。
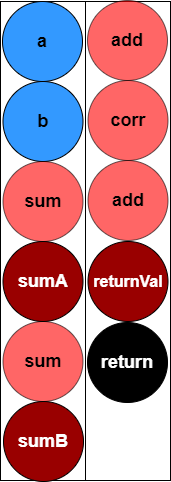
在执行节点时,如果当前节点是一个算子节点,首先会判断这个算子是在 CPU 执行还是 GPU 执行,紧接着会把算子依赖的参数,拷贝到相应的位置(CPU 或者 GPU)。拷贝任务全部交由数据传输模块完成。当算子依赖的参数被拷贝完成后,算子节点会执行这个算子,调用 GPU 进行加速。
当工作队列为空时,代表整个计算图的用户自定义函数执行结束。然后 Shark Graph 会将返回值从 GPU 拷贝到内存,然后返回给用户。
2.3 快速上手:vwap 指标计算
快速部署测试环境:
- 申请 Shark 测试 License:社区版 License 暂不支持 Shark,如需使用,请前往官网下载页面,点击 Shark 产品的“试用 License”,申请对应 License。
- 下载 Shark 安装包:请前往官网下载页面选择 Shark 页面的立即下载。
- 部署流程请参照单节点部署与集群部署。
- 部署在一台支持 GPU 的服务器上,当前版本支持 GPU 型号如下:
- Nvidia:要求显卡的计算能力达到 6.0 或以上,请查阅 Nvidia 官方文档。
vwap 指标计算示例代码如下。
- 准备矩阵格式的模拟行情数据(价格、成交量)
def simulation(days, nSymbols){ """ 生成price & volume模拟数据 """ // 模拟交易时间生成, 假设早盘9点半-11点半,下午1点-3点 timeList = (09:30:00 + 3*0..2400) <- (13:00:00 + 3*0..2400) timeList = each(concatDateTime{, timeList}, days).flatten() // 获取时间戳总长度 nTimes = size(timeList) // 模拟价格矩阵 // 给每个标的随机设置一个初始价格 initPrice = rand(100.0, nSymbols) initPriceMatrix = flip(take(initPrice, nSymbols*nTimes)$nSymbols:nTimes) // 给每个标的随机设置一个收益率序列 returnMatrix = norm(0, 0.01, nTimes:nSymbols) // 计算模拟价格矩阵 priceMatrix = initPriceMatrix * cumprod(1 + returnMatrix) priceMatrix.rename!(string(timeList), "c"+lpad(string(1..nSymbols), 6, "0")) priceMatrix = round(priceMatrix, 3) // 模拟成交量矩阵 volumeMatrix = 100*rand(100, nSymbols*nTimes)$nTimes:nSymbols volumeMatrix.rename!(string(timeList), "c"+lpad(string(1..nSymbols), 6, "0")) return priceMatrix, volumeMatrix } // 模拟日期 days = 2025.01.01 // 模拟标的数量 nSymbols = 6000 // 生成模拟数据 price, volume = simulation(days, nSymbols) - 编写 CPU 版本与 GPU 版本的 vwap 指标计算脚本,若函数均使用 Shark Graph 目前支持的数据格式与聚合函数,则可以直接添加
@gpu注解使得 DolphinDB 脚本调用 GPU 加速运算。def vwap_cpu(price, volume, window){ result = msum(price * volume, window) / msum(volume, window) return result } @gpu def vwap_gpu(price, volume, window){ result = msum(price * volume, window) / msum(volume, window) return result } - 运行,并查看对应性能比较
// CPU 运行耗时 timer{ result = vwap_cpu(price, volume, 20) } // GPU 运行耗时 timer{ result = vwap_gpu(price, volume, 20) }
输出结果为如下所示,可以看出,使用 Shark Graph 加速的函数运行效率远远高于单纯使用 CPU 进行运算的函数。
// CPU 运行耗时
Time elapsed: 444.387 ms
// GPU 运行耗时
Time elapsed: 40.881 ms3. 应用案例
3.1 背景介绍
3.1.1 雪球期权典型案例
雪球产品是一类典型的自动赎回结构化产品,当标的资产的价格在特定日期超过某约定的水平时,产品触发自动赎回。因为雪球产品通常能够提供较高的票息,所以近年来得到了广大投资者的青睐,市场规模不断扩张。雪球期权作为雪球产品的重要组成部分,其期权结构本质是投资者卖出了带有复杂障碍条件的看跌期权:当标的资产上涨的时候获得有限制的收益,但当标的资产下跌的时候,可能承担和资产相同的跌幅。
面向对于雪球期权了解不多的读者,本文以一个经典的雪球期权合约为例,讲解雪球期权合约与传统多头或指数基金的损益差别,以便更好地理解后续内容。下表展示了一个典型的雪球期权合约结构以及具体参数:
| 产品要素 | 要素性质 |
|---|---|
| 标的资产 | 中证500指数(000905.SH) |
| 观察期限 | 1 年,从第三个月开始每月末观察敲出+每日观察敲入 |
| 期权结构 | 自动敲入敲出结构 |
| 名义本金 | 100万 |
| 敲出水平 | 期初价格*103% |
| 敲入水平 | 期末价格*80% |
| 敲出票息 | 25%(年化) |
| 红利票息 | 25%(年化) |
| 敲出事件 | 任意敲出观察日,挂钩标的收盘价≥敲出水平 |
| 敲入事件 | 任意敲入观察日,挂钩标的收盘价<敲入水平 |
| 收益计算 | 敲出(自动提前终止):25%*名义本金*(计息天数/365) |
| 未敲入未敲出(延续至期末):25%*名义本金*(计息天数/365) | |
| 敲入且未敲出(标的期末价格小于期初价格):(期末价格/期初价格-1)*名义本金 | |
| 敲入且未敲出(标的期末价格处于期初价格与敲出价格之间):0 |
对于以上典型的雪球期权合约,假设作为雪球期权的买方,最终的损益情况可以分为三种:
- 提前敲出:说明中证指数在3个月后的月频敲出观察日中某一个的收盘价 ≥ 期初价格 * 103% ,此时触发敲出条件,按照敲出票息进行结算,获得本金+25%票息
- 未敲入且未敲出:说明中证500指数在3个月后的所有月频敲出观察日的收盘价 < 期初价格 * 103%,同时日频敲入观察日的收盘价均 ≥ 期初价格 * 80%,此时既没有触发敲入条件,也没有触发敲出条件,按照红利票息进行结算,依然获得本金+25%票息
- 敲入后未敲出,即中证500指数3个月后在某一个日频敲入观察日的收盘价 < 期初价格 * 80%,同时月频敲出观察日的收盘价均 < 期初价格 * 103%,此时仅触发敲入条件而没有触发敲出条件,雪球期权亏损为 min((期末价格/期初价格-1),0) * 名义本金。假设期末价格为 St,期初价格为 S0,敲入且未敲出时合约到期的收益为 -max(S0-St,0),相当于投资者卖出了一份行权价为 S0 的看跌期权的损益。
因而,将不同的雪球期权损益情形总结起来,就是下图流程图展示的损益结算规则:
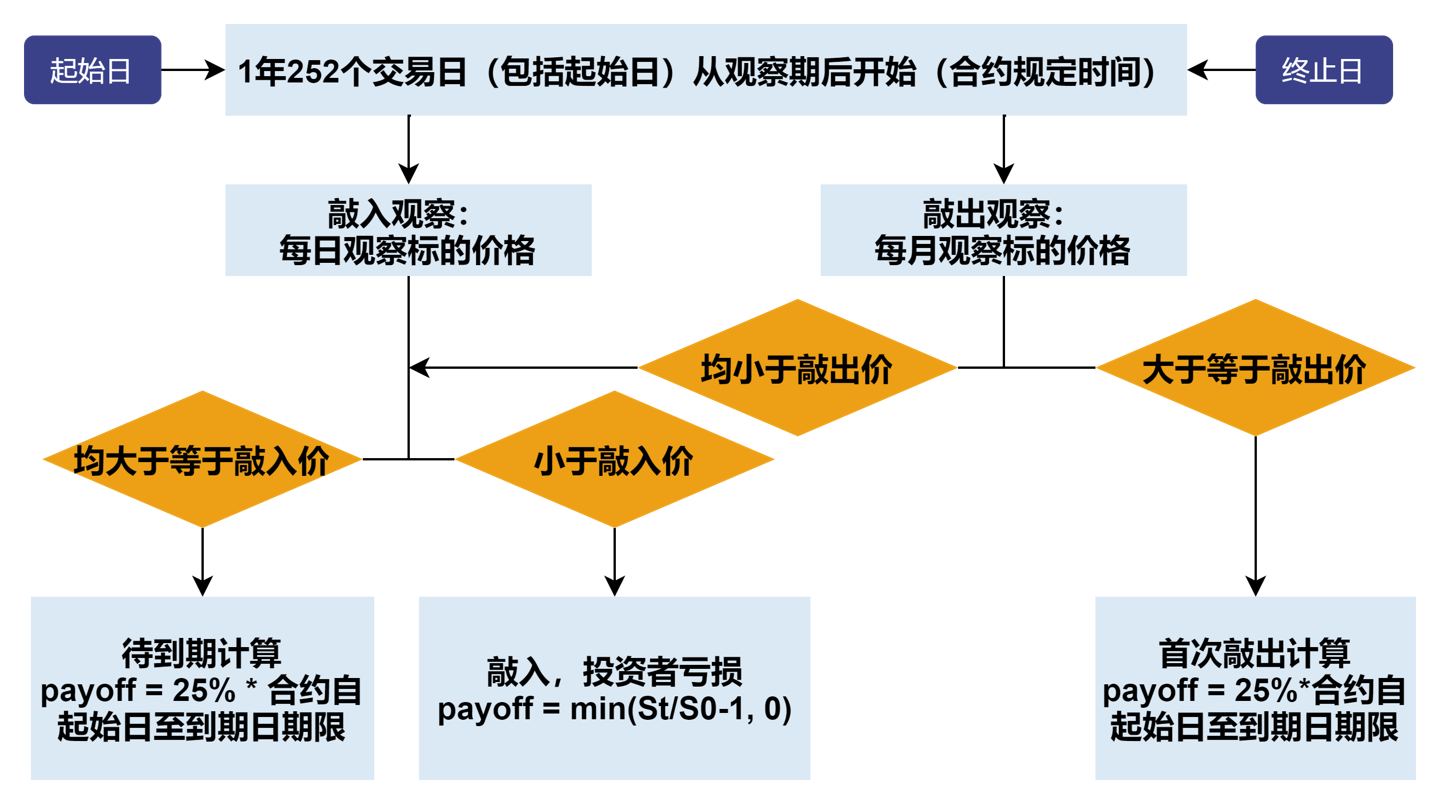
同时,对于雪球期权的发行方而言,其损益与上述买方损益恰好相反。雪球期权发行方的目标是在给定目标利润率与其他参数的情况下,为其发行的雪球期权产品制定合适的票息率。
3.1.2 期权定价模型
对于期权的数值定价方法,主要有 BS 公式法,有限差分法与蒙特卡洛法三种方法。BS 方法是期权定价的经典解析方法,其核心思想是通过构建无风险对冲组合,推导出期权价格满足的 PDE ,并求得闭式解。有限差分即是对期权 PDE 中的偏导用有限差分替代,进而通过构造网格求解三对角方程组的方式求解出期权本身的价值,但其计算方法相对复杂。蒙特卡洛则是通过假设标的资产价格为某个随机过程并大量模拟该随机过程下的轨道,进而得到期权的数值解。其优点一是实现起来非常简单,二是由于误差收敛率不依赖于问题的维数,从而非常适用于高维期权定价,常用于路径依赖 (path-dependent) 的各类奇异期权,以及多资产期权 (multi-asset) 模型。
本文所介绍的雪球期权属于奇异期权,其定价通常依赖于蒙特卡洛模拟方法,蒙特卡洛方法实现期权定价的基本原理如下:
假设风险中性测度下,资产价格服从 GBM (Geometric Brownian Motion, 几何布朗运动),则满足:
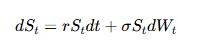
其中:St 为 t 时刻的资产价格,r 为无风险利率,σ 为资产价格的波动率,Wt 为维纳过程。在离散时间形式下,雪球期权对应标的资产价格路径可以通过以下公式生成:
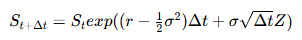
在模拟出价格路径的情况下,雪球期权买方仅需根据模拟出的价格路径,按照雪球期权损益规则计算期权现值,对不同价格路径对应的现值取均值即可得到雪球期权的价值:
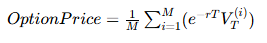
对于雪球期权的发行方而言,其目标是给定利润率计算雪球的票息率(敲出票息与红利票息),仍然遵循上述步骤模拟出价格路径并计算雪球现值。之后可利用二分法等数值方法对票息率进行逼近,从而求出满足目标收益率的票息率。
3.2 场景1:雪球期权定价
基于上文介绍的蒙特卡洛模拟方法进行雪球期权的定价方法,具体雪球期权定价的实现逻辑如下图所示:
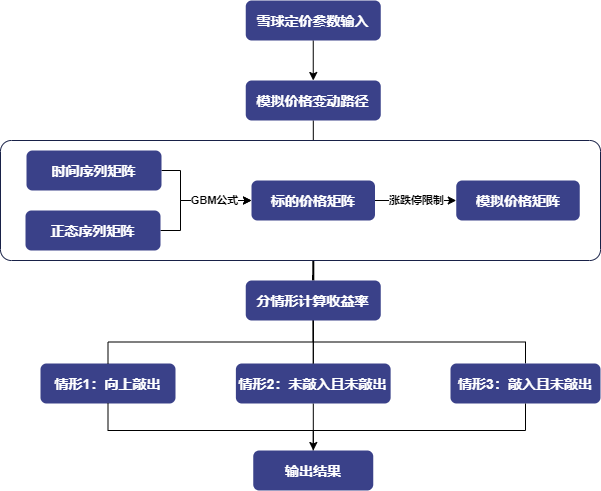
3.2.1 路径模拟
利用 seq 函数与 repmat 函数构造指定数量的时间序列矩阵,并利用 norm 函数生成正态分布矩阵,将时间序列矩阵与正态分布矩阵带入 Black Sholes 公式构造标的价格矩阵。进一步地,本案例设置了一定的涨跌幅限制(这里是日上下10%),从而更贴合实际交易环境。该部分的实例代码如下所示:
@gpu
def simulation(S, r, T, sigma, N, days_in_year){
// 计算每日时间间隔, 折算成年的时间差
dt = 1 \ days_in_year
// 计算到期时间, 折算成日
Tdays = T*days_in_year
// 月交易日数 (每个月观察一次是否敲出)
monthDay = int(days_in_year/12)
all_t = dt*(0..Tdays)
// 一列是一个时间序列,有 N 列
dtMatrix = repmat(matrix(all_t),1,N)
normMatrix = norm(0,1,(Tdays+1)*N)$(Tdays+1):N
normMatrix = normMatrix * (all_t>0)
// 一列是一个价格路径,有 N 列
ST = S * exp((r-0.5*sigma*sigma)*dtMatrix + sigma*sqrt(dt)*cumsum(normMatrix))
Spath = ST[1..Tdays, ]
// 进行涨跌停限制
prevPrice = ST[0..(Tdays-1), ]
uplimit = prevPrice*1.1
lowlimit = prevPrice*0.9
Spath = iif(Spath > uplimit, uplimit, iif(Spath < lowlimit, lowlimit, Spath))
return Spath
}模拟出的价格路径矩阵 Spath 的可视化如图所示,这里只展示前 25 条标的价格路径。
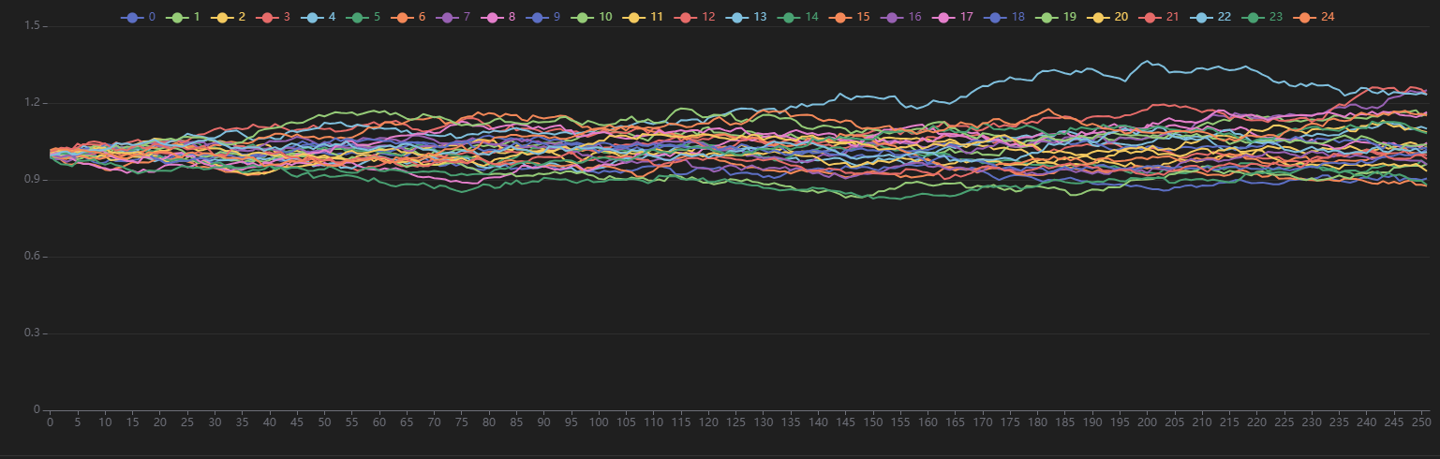
3.2.2 定价函数
如上文所介绍,用户对于仅使用 Shark Graph 支持数据格式与相关函数的函数加上
@gpu
注解,即可使用DolphinDB 脚本在 GPU 上加速计算。在获得标的价格矩阵后,可以利用 DolphinDB
的向量化编程,对于雪球期权每条价格路线的损益状态进行向量化判断,得到每一条价格路径的雪球期权现值,取均值即为最终雪球期权的定价结果。
以下是 Shark 雪球期权定价的主体函数,该函数会返回每一条雪球期权价值组成的向量 payoff,向下敲入次数 knock_in_times ,向上敲出次数 knock_out_times ,正常到期次数 existence_times 与亏损次数 lose_times :
@gpu
def snowball_pricing(S,r,T,sigma,N,coupon,k_out,k_in,lock_period,days_in_year){
// 计算到期时间, 折算成日
Tdays = T*days_in_year
// 月交易日数 (每个月观察一次是否敲出)
monthDay = int(days_in_year/12)
Spath = simulation(S, r, T, sigma, N, days_in_year)
// 构造需要观察是否敲入的时间序列(超过封闭期)
observation_out_idx = monthDay*(1..(Tdays/monthDay))
observation_out_idx = observation_out_idx[observation_out_idx>lock_period]-1
// 判断每个月是否需要敲出
knockOutMatrix = Spath[observation_out_idx, ]>=k_out
// 获取敲出的日期
knock_out_day = observation_out_idx*knockOutMatrix
// 计算首次敲出的日期
knock_out_day = min(knock_out_day[knock_out_day>0])
// 判断是否需要敲入
knock_in_day = sum(Spath < k_in)
// 计算收益率:
// 情景1:发生了向上敲出事件: 此时按照合约规定,该雪球类产品提前终止
// 投资者收益=年化票息率*合约持有期限年化
payoff1 = coupon*knock_out_day/days_in_year*exp(-r * knock_out_day/days_in_year)
// 情景2:未敲出且未敲入: 此时按照合约规定, 该雪球类产品到期自动终止
// 投资者收益=年化票息率*合约持有期限年化
payoff2 = coupon * exp(-r * T)
// 情景3:只发生向下敲入,不发生向上敲出, 且合约到期时,标的价格低于期初标的价格
// 此时按照合约规定,该雪球类产品到期自动终止,此时敲入的看跌期权为实值,投资者需要承担标的下跌造成的损失。
payoff3 = (last(Spath) - S)*exp(-r * T)
// 判断每一个价格路径的收益状态
payoff = iif(knock_out_day>0, payoff1,
iif(knock_in_day==0, payoff2,
iif(last(Spath)<S, payoff3, 0)))
// 统计敲出次数:
knock_out_times = sum(knock_out_day>0)
// 统计未敲出且未敲入次数
existence_times = sum(knock_out_day<=0&&knock_in_day==0)
// 统计敲入次数
knock_in_times = sum(knock_out_day<=0&&knock_in_day>0)
// 统计亏损次数
lose_times = sum(knock_out_day<=0&&knock_in_day>0&&last(Spath)<S)
return payoff, knock_out_times, knock_in_times, existence_times,lose_times
}3.2.3 函数参数
蒙特卡洛方法进行雪球期权定价的模拟路径数量、标的初始价格、敲入边界价格、敲出边界价格、标的波动率等均可以通过参数进行配置,本案例所用到的雪球期权定价参数含义如下表所示:
| 参数名称 | 参数变量 | 参数解释 | |
|---|---|---|---|
| 1 | 模拟路径条数 | N | 蒙特卡洛方法模拟出的资产价格变动路径条数 |
| 2 | 初始价格 | S | 雪球期权对应标的的初始价格 |
| 3 | 年交易日数量 | days_in_year | 一年中的交易日总数 |
| 4 | 观察期 | lock_period | 雪球期权合约规定的观察期天数 |
| 5 | 敲入边界 | k_in | 雪球期权合约规定的敲入边界价格 |
| 6 | 敲出边界 | k_out | 雪球期权合约规定的敲出边界价格 |
| 7 | 无风险利率 | r | 用户设置的无风险收益率 |
| 8 | 到期时间 | T | 雪球期权对应的到期时间,单位为年 |
| 9 | 波动率 | sigma | 用户设置的标的年化波动率 |
| 10 | 贴水利率 | coupon | 雪球期权对应的年化票息率(这里假设敲出票息=红利票息) |
参数配置与具体的运行代码如下所示:
N = 300000 // 模拟路径数量
S = 1.0 // 标的初始价格
k_in = 0.85 // 敲入边界
k_out = 1.03 // 敲出边界
T = 1 // 到期时间(年)
days_in_year = 252 // 一年的交易日数
sigma = 0.13 // 标的波动率(年化)
r = 0.03 // 无风险利率(年化)
coupon = 0.2 // 贴水利率(年化)
lock_period = 90 // 锁仓期(日)
timer payoff, knock_out_times, knock_in_times, existence_times, lose_times = snowball_pricing(S, r, T, sigma, N, coupon, k_out, k_in, lock_period, days_in_year)
print("雪球价值:", avg(payoff))
print("敲出概率:", knock_out_times \ N)
print("未敲入也未敲出概率:", existence_times \ N)
print("敲入且未敲出概率:", knock_in_times \ N)
print("亏损概率:", lose_times \ N)3.2.4 定价结果
使用 Shark Graph 加速运算的输出结果如下所示,可以看出,以上参数对应的雪球期权预期收益率为 5%,敲出概率为 73%,具备一定的投资价值,雪球期权定价的运行速度不到 40ms。
Time elapsed: 36.827 ms
雪球价值:
0.050549256728865
敲出概率:
0.737543333333333
未敲入也未敲出概率:
0.136706666666667
敲入且未敲出概率:
0.12575
亏损概率:
0.1237766666666673.3 场景2:雪球期权设计
基于上文介绍的给定利润率的雪球期权的票息率确定方法,雪球期权卖方票息率的确定逻辑如下图所示:
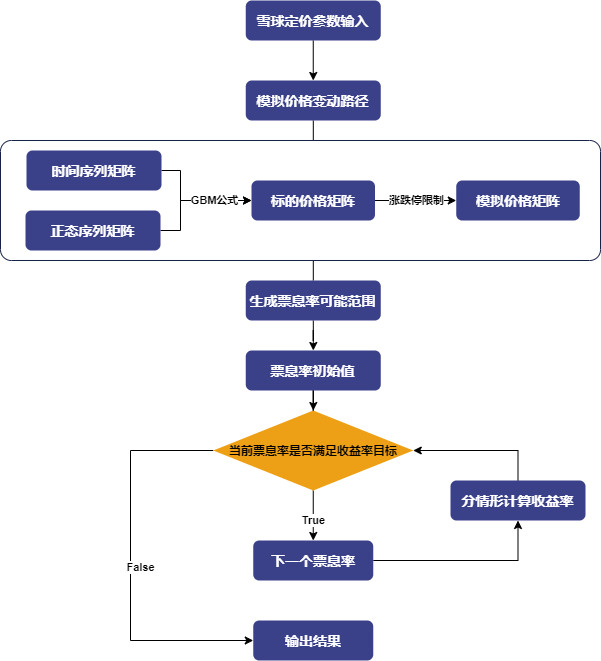
3.3.1 票息率确定相关函数
首先,不同于雪球期权定价,给定利润率进行雪球期权票息率的确定需要利用数值方法对相同的价格矩阵进行雪球价值计算,因而首先单独定义雪球价值计算函数,依然使用
@gpu 注解利用 Shark Graph 进行 GPU 加速计算:
@gpu
def calculate_pay_off(coupon, Spath, S, r, T, knock_out_day, knock_in_day, days_in_year){
// 分三种情景计算收益率:
payoff1 = coupon * knock_out_day / days_in_year * exp(-r * knock_out_day / days_in_year)
payoff2 = coupon * exp(-r * T)
payoff3 = (last(Spath) - S)*exp(-r * T)
// 判断每一个价格路径的收益状态
payoff = iif(knock_out_day>0, payoff1,
iif(knock_in_day==0, payoff2,
iif(last(Spath)<S, payoff3, 0)))
return payoff
}之后,这里使用了等距网格搜索,固定间隔生成雪球期权票息率的可能范围,间距为 0.001,在此基础上进行搜索票息率,直至前后两个票息率对应的现值刚好包含了发行方期望的现值:
@gpu
def snowball_pricing(S, r, T, sigma, N, k_out, k_in, lock_period, days_in_year, profit_rate){
Tdays = T*days_in_year
monthDay = int(days_in_year/12)
Spath = simulation(S, r, T, sigma, N, days_in_year) // 模拟价格路径矩阵
observation_out_idx = monthDay*(1..(Tdays/monthDay))
observation_out_idx = observation_out_idx[observation_out_idx>lock_period]-1
knockOutMatrix = Spath[observation_out_idx, ]>=k_out
knock_out_day = observation_out_idx*knockOutMatrix
knock_out_day = min(knock_out_day[knock_out_day>0])
knock_in_day = sum(Spath < k_in)
knock_out_times = sum(knock_out_day>0) // 模拟价格路径发生敲入的数量
existence_times = sum(knock_out_day<=0&&knock_in_day==0) // 模拟价格路径发生未敲入未敲出的数量
knock_in_times = sum(knock_out_day<=0&&knock_in_day>0) // 模拟价格路径发生期末敲入未敲出的数量
lose_times = sum(knock_out_day<=0&&knock_in_day>0&&last(Spath)<S) // 投资者亏损次数(发行方盈利次数)
// 固定间隔生成票息率可能范围
coupon_test_range = (0..1000)*0.001 // 精确到小数点后四位
// for loop循环搜索
lastvalue = 0
lastcoupon = 0
target = (1-profit_rate)
for (coupon in coupon_test_range){
// 计算路径对应的现值
value = 1.0 + avg(calculate_pay_off(coupon, Spath, S, r, T, knock_out_day, knock_in_day, days_in_year))
if (value > target > lastvalue){
break
}
lastvalue = value
lastcoupon = coupon
}
// 获取区间边界
coupon_lower_bound = lastcoupon // coupon上边界
coupon_upper_bound = coupon // coupon下边界
return 0.5*(coupon_lower_bound + coupon_upper_bound), knock_out_times, knock_in_times, existence_times, lose_times
}3.3.2 函数参数
下表列示了用于确定雪球发行方票息率的函数的相关参数,除了profit_rate 参数其余参数均与雪球定价函数的参数保持一致。
| 参数名称 | 参数变量 | 参数解释 | |
|---|---|---|---|
| 1 | 模拟路径条数 | N | 蒙特卡洛方法模拟出的资产价格变动路径条数 |
| 2 | 初始价格 | S | 雪球期权对应标的的初始价格 |
| 3 | 年交易日数量 | days_in_year | 一年中的交易日总数 |
| 4 | 观察期 | lock_period | 雪球期权合约规定的观察期天数 |
| 5 | 敲入边界 | k_in | 雪球期权合约规定的敲入边界价格 |
| 6 | 敲出边界 | k_out | 雪球期权合约规定的敲出边界价格 |
| 7 | 无风险利率 | r | 用户设置的无风险收益率 |
| 8 | 到期时间 | T | 雪球期权对应的到期时间,单位为年 |
| 9 | 波动率 | sigma | 用户设置的标的年化波动率 |
| 10 | 预期利润率 | profit_rate | 雪球发行方预期的利润率水平(这里不考虑发行成本) |
参数配置与具体的运行代码如下所示:
N = 300000 // 模拟路径条数
S = 1.0 // 标的初始价格
k_in = 0.85 // 敲入边界
k_out = 1.03 // 敲出边界
T = 1 // 到期时间(年)
days_in_year = 252 // 一年的交易日数
sigma = 0.13 // 标的波动率(年化)
r = 0.03 // 无风险利率(年化)
lock_period = 0 // 锁仓期(日)
profit_rate = 0.01 // 雪球期权发行方目标利润率
timer coupon, knock_out_times, knock_in_times, existence_times, lose_times = snowball_pricing(S, r, T, sigma, N, k_out, k_in, lock_period, days_in_year, profit_rate)
print("雪球票息率:", coupon)
print("敲出概率:", knock_out_times \ N)
print("未敲入也未敲出概率:", existence_times \ N)
print("敲入且未敲出概率:", knock_in_times \ N)
print("发行方盈利概率:", lose_times \ N) // 发行方盈利概率=买方亏损概率3.3.3 定价结果
使用 Shark Graph 加速运算的输出结果如下所示,可以看出,以上参数对应的雪球期权票息率为 2.35%。
Time elapsed: 116.619 ms
雪球票息率:
0.0235
敲出概率:
0.7385
未敲入也未敲出概率:
0.135646666666667
敲入且未敲出概率:
0.125853333333333
亏损概率:
0.123934. 性能测试
4.1 性能测试结果
为了更清晰地展现 DolphinDB CPU-GPU 异构计算平台 Shark 的强大性能,基于前述内容,本节我们编写了分别使用 DolphinDB Shark GPU、Python 以及 R 语言进行性能比对,仍然模拟30万条标的价格路径进行计算。
表 4-1 雪球期权定价性能测试结果
| 软件 | 版本 | 雪球期权定价耗时(ms) | 性能提升(倍数) | |
|---|---|---|---|---|
| 1 | DolphinDB Shark GPU | 3.00.3 2025.05.15 LINUX_ABI x86_64 | 36 | \ |
| 2 | Python+JIT | 3.12.7 | 1,054 | 29 |
| 3 | Python | 3.12.7 | 5,935 | 165 |
| 4 | R | 4.5.1 | 19,816 | 550 |
表 4-2 雪球期权票息率确定性能测试结果
| 软件 | 版本 | 雪球期权票息率确定耗时(ms) | 性能提升(倍数) | |
|---|---|---|---|---|
| 1 | DolphinDB Shark GPU | 3.00.3 2025.05.15 LINUX_ABI x86_64 | 116 | \ |
| 2 | Python+JIT | 3.12.7 | 1,213 | 10 |
| 3 | Python | 3.12.7 | 6,497 | 56 |
| 4 | R | 4.5.1 | 20,518 | 177 |
同时为了进一步探究模拟路径个数对于定价结果以及运行时间的影响,我们从1万条开始遍历蒙特卡洛模拟价格路径至50万条,间距为1万,仍然利用以上四种方式进行雪球期权蒙特卡洛定价,并绘制毫秒耗时与计算得到的雪球期权价值。
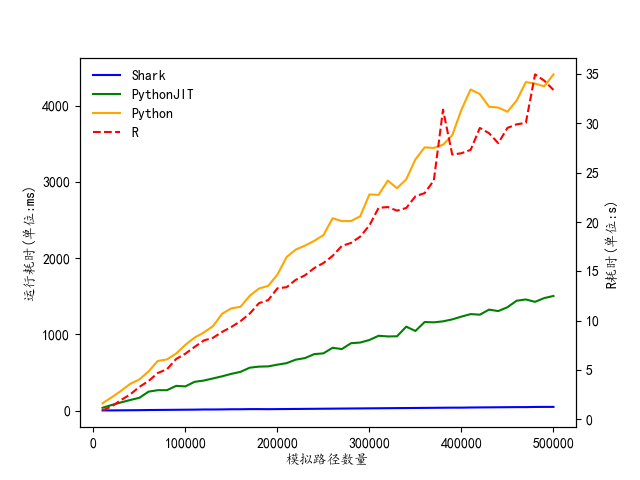
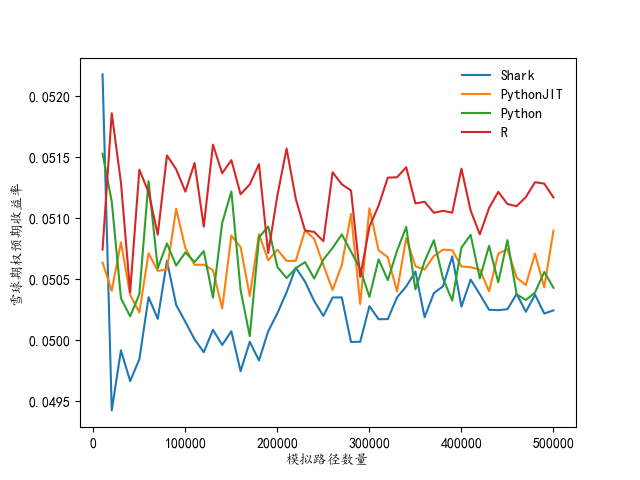
对于雪球期权的票息率确定,采用同样的方式进行性能比较,依然从1万条开始遍历蒙特卡洛模拟价格路径至50万条,间距为1万,并绘制毫秒耗时与给定目标参数计算得到的雪球票息率。
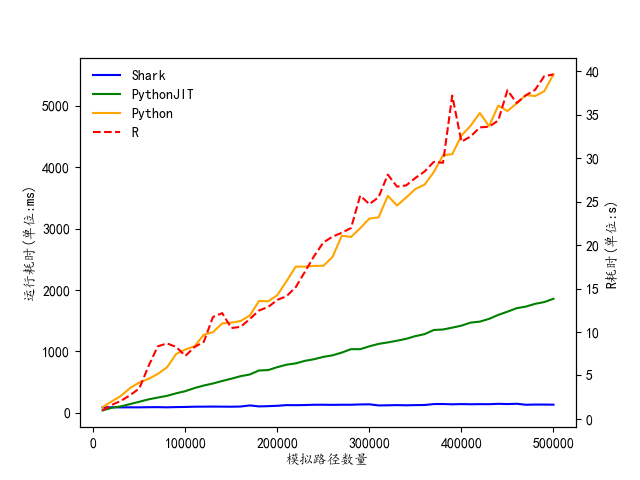
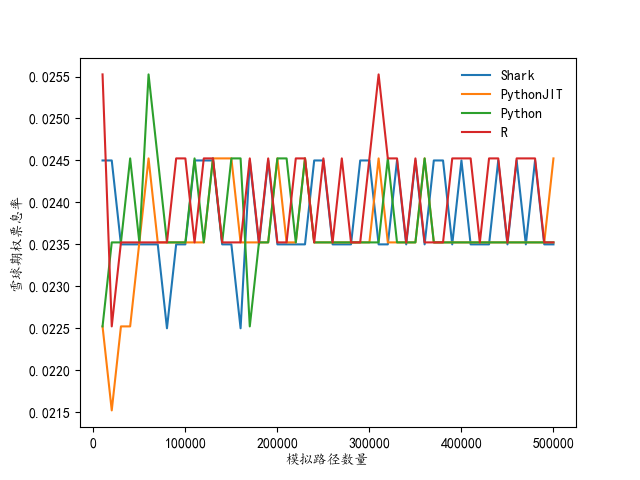
从上述图表中可以看出,分别采用 DolphinDB Shark GPU、Python+JIT、单纯 Python 与 R 语言所得出的雪球期权定价、票息率确定结果均一致,但运行速度差距较大。其中 DolphinDB Shark GPU版本的计算性能最佳,在50万条标的价格路径时雪球期权定价仅耗时36ms,同时给定目标利润率的情况下完成雪球期权票息率确定仅需 116ms,充分展示了DolphinDB Shark GPU 版本的强大性能与在 FICC 领域应用的巨大潜力。
4.2 测试环境配置
安装 DolphinDB server,配置为集群模式。本次测试所涉及到的硬件环境和软件环境如下:
- 硬件环境
| 硬件名称 | 配置信息 |
|---|---|
| 内核 | 3.10.0-1160.88.1.el7.x86_64 |
| CPU | Intel(R) Xeon(R) Gold 5220R CPU @ 2.20GHz |
| GPU | NVIDIA A30 24GB(1块) |
| 内存 | 512GB |
- 软件环境
| 软件名称 | 版本及配置信息 |
|---|---|
| 操作系统 | CentOS Linux 7 (Core) |
|
DolphinDB |
server 版本:3.00.3 2025.05.15 LINUX x86_64 |
| license 限制:16 核 128 GB |
5. 总结
本文基于 DolphinDB CPU-GPU 异构计算平台 Shark 的计算图功能,完整实现了雪球期权定价和票息率确定两大应用场景。DolphinDB 将自身强大的运算性能与期权定价的具体实践场景相结合,展现了 DolphinDB 在 FICC 领域的强大应用能力,能够帮助用户更快更精准地对于雪球期权的价值进行确定与判断。
