socp
语法
socp(f, [G], [h], [l], [q], [Aeq], [beq])
详情
该函数用于求解二阶锥规划问题,计算目标函数在限定条件下的最小值。若其约束条件以标准形式给出,其形式如下:
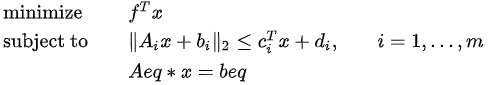
则矩阵 G 为:
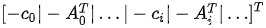
向量 h 为:
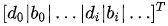
参数
二阶锥规划(Second-Order Cone Programming,SOCP)问题的约束条件形式如下:
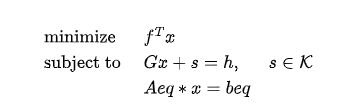
其中 K 为锥,s 为松弛变量,其值在优化过程中会被确定。
f 是数值型向量,表示目标函数的系数向量。
G 是数值型矩阵,表示锥约束的系数矩阵。
h 是数值型向量,表示锥约束的右端向量。
l 是整数标量,表示非负象限约束的维度。
q 是正数向量,表示各个二阶锥约束的维度大小,形式为 [r0,r1,…,rN-1]。
Aeq 是数值型矩阵,表示等式约束的系数矩阵。
beq 是数值型向量,表示等式约束的右端向量。
返回值
返回一个长度为 3 的元组:
- 第一个元素表示求解状态描述。
Exitcode 状态描述 0 Optimal solution found 1 Certificate of primal infeasibility found 2 Certificate of dual infeasibility found 10 Optimal solution found subject to reduced tolerances 11 Certificate of primal infeasibility found subject to reduced tolerances 12 Certificate of dual infeasibility found subject to reduced tolerances -1 Maximum number of iterations reached -2 Numerical problems (unreliable search direction) -3 Numerical problems (slacks or multipliers outside cone) -7 Unknown problem in solver - 第二个元素是目标函数取最小值时 x 的取值。
- 第三个元素是目标函数的最小值。
例子
求解以下二阶锥规划问题:
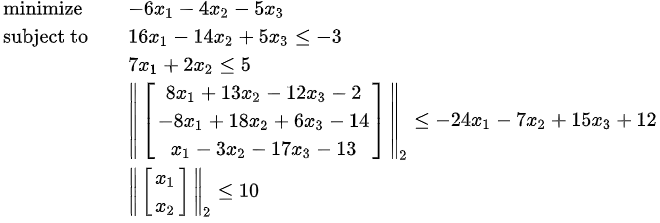
f = [-6, -4, -5]
G = matrix([[16, 7, 24, -8, 8, -1, 0, -1, 0],
[-14, 2, 7, -13, -18, 3, 0, 0, -1],
[5, 0, -15, 12, -6, 17, 0, 0, 0]])
h = [-3, 5, 12, -2, -14, -13, 10, 0, 0]
l = 2
q = [4,3]
re = socp(f,G,h,l,q, ,)
print(re)返回:("Optimal solution found",[-9.902804882871327,-1.39084684264198,26.211851780740154],-66.079042235904907)
