linprog
语法
linprog(f, [A], [b], [Aeq], [beq], [lb], [ub], [method='simplex'])
详情
求线性目标函数在约束条件下的最优解。具体模型如下:
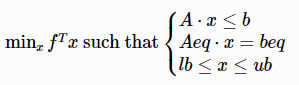
返回结果是具有两个元素的元组。第一个元素是目标函数的最小值,第二个元素是目标函数取最小值时,x的取值。
参数
f 是线性规划中的一次项向量。
A 是线性不等约束的系数矩阵。
b 是线性不等约束的右端向量。
Aeq 是线性等式约束的系数矩阵。
beq 是线性等式约束的右端向量。
lb 表示变量的下界。
ub 表示变量的上界。
method 是字符串,表示算法,目前支持 'simplex' 和 'interior-point'。推荐使用 simplex 算法,部分特殊场景下建议使用 interior-point 算法。
linprog 函数的参数有以下要求:
-
A 和 Aeq 必须是列数相同的矩阵
-
f, b 和 beq 是向量
-
lb 和 ub 可以是标量,也可以是和x等长的向量。
-
若 lb 或 ub 是标量,则所有变量都受同一个下界或上界约束。若 lb 或 ub 为NULL,表示x无相应的下界或上界约束。
-
若 lb 或 ub 是向量,则x中的元素受 lb 或 ub 中相应位置的元素约束。若向量 lb 或 ub 中某元素为NULL,表示此位置的x元素无相应的下界或上界约束
-
例子
例1. 求 x,y 满足以下约束条件时,目标函数 x+2y 的最小值。
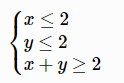
f = [1, 2];
A = [-1, -1]$1:2;
b = [-2];
ub = 2;
re = linprog(f, A, b, , , , ub);
re[0];
# output
2
re[1];
# output
[2,0]下面详细解释如何获取上例中的 A, b 和 ub。不等式约束条件为 x+y>=2,而模型中的不等式约束条件的符号为<=,因此需要转换成 -x-y<=-2。因此,不等式约束条件的系数矩阵为 [-1,-1]$1:2,不等式约束条件的右端向量为-2。变量 x, y 的上界都是2,因此 ub 可用标量表示。
例2. 求 x,y 满足以下约束条件时,目标函数 -3x1-2x2 的最小值。
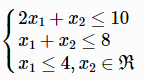
f = [-3, -2];
A = [2, 1, 1, 1]$2:2;
b = [10, 8];
ub = [4, NULL];
re = linprog(f, A, b, , , , ub);
re[0];
# output
-18
re[1];
# output
[2,6]