quadprog
语法
quadprog(H, f, [A], [b], [Aeq], [beq])
参数
H 是二次规划中的二次项矩阵,且必须是对称正定矩阵。
f 是二次项规划中的一次项向量。
A 是线性不等约束的系数矩阵。
b 是线性不等约束的右端向量。
Aeq 是线性等式约束的系数矩阵。
beq 是线性等式约束的右端向量。
H, A 和 Aeq 必须是列数相同的矩阵。
f, b 和 beq 是向量。
详情
求二元目标函数在线性约束条件下的最优解。具体模型如下:
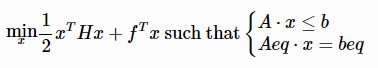
返回结果是具有两个元素的元组。第一个元素是目标函数的最小值,第二个元素是目标函数取最小值时,x的取值。
例子
求以下目标函数的最小值。
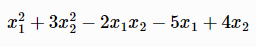
例1:没有约束条件
H=matrix([2 -2,-2 6])
f=[-5,4]
x=quadprog(H,f);
x[0];
# output
-6.375
x[1];
# output
[2.75,0.25]例2:添加不等式约束条件:
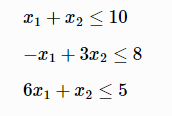
H=matrix([2 -2,-2 6])
f=[-5,4]
A=matrix([1 -1 6, 1 3 1])
b=[10, 8, 5]
x=quadprog(H,f,A,b);
x[0];
# output
-4.092975
x[1];
# output
[0.904959, -0.429752]例3:添加不等式约束条件和等式约束条件:
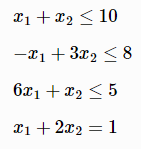
H=matrix([2 -2,-2 6])
f=[-5,4]
A=matrix([1 -1 6, 1 3 1])
b=[10, 8, 5]
Aeq=matrix([1],[2])
beq=[1]
x=quadprog(H,f,A,b,Aeq,beq);
x[0];
# output
-3.181818
x[1];
# output
[0.818182,0.090909]目标函数在没有约束条件的情况下,最优解的值最小。约束条件越多,最优解的值越大。
