lassoBasic

语法

lassoBasic(Y, X, [mode=0], [alpha=1.0], [intercept=true], [normalize=false], [maxIter=1000], [tolerance=0.0001], [positive=false], [swColName], [checkInput=true])

详情

进行 lasso 回归估计。最小化以下目标函数：


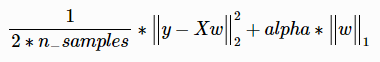
lasso

参数

Y 数值类型的向量，表示因变量。

X 数值类型的向量/元组/矩阵/表，表示自变量。

  • 当 X 是向量/元组时，其长度必须等于 Y 的长度。

  • 当 X 是矩阵/表时，其行数必须等于 Y 的长度。

mode 一个整数，可取以下 3 个值:

  • 0（默认值）: 输出一个系数估计向量

  • 1: 输出一个具有系数估计，标准差，t 统计量和 p 值的表

  • 2: 输出一个具有 ANOVA（方差分析）、RegressionStat（回归统计）、Cofficient（系数）和 Residual（残差）的字典，具体含义见下表：

键 ANOVA 对应值：

Source of Variance 自由度(Degree of freedom) 平方和(Sum of Square) 均方差(Mean of square) F统计量 Significance
Regression（回归） 变量个数（p） 回归平方和（SSR） 回归均方差（MSR=SSR/R） MSR 对 MSE 的比值 显著性，即统计出的P值
Residual（残差） 残差自由度（n-p-1） 残差平方和（SSE） 残差均方差（MSE=MSE/E）
Total 样本自由度， 不包括常数项（n-1） 总离差平方和（SST）

键 RegressionStat 对应值：

item 统计值
R2 R 决定系数，描述回归曲线对真实数据点拟合程度的统计量。范围在 [0,1]之间，越接近1 ，说明对y的解释能力越强，拟合越好。
AdjustedR2 经自由度修正后的决定系数，通过样本数量与模型数量对 R-squared 进行修正。
StdError 回归残差标准误差，残差经自由度修正后的标准差。
Observations 观察样本个数。

键 Coefficient 对应值：

元素 说明
factor 自变量名称
beta 回归系数估计值
stdError 回归系数标准误差。
tstat T 统计值，衡量系数的统计显著性。

键 Residual 对应每一个预测值和实际值之间的残差。

alpha 一个浮点数，表示乘以 L1 范数惩罚项的系数。默认值是1.0。

intercept 布尔值，表示是否包含回归中的截距。默认值为 true，此时系统自动给 X 添加一列 “1” 以生成截距。

normalize 布尔值，默认值为 false。若设为 true，则所有自变量均会进行如下标准化：减去平均值，然后除以 L2 范数。若 intercept 为 false，该参数会被忽略。

maxIter 一个正整数，表示最大迭代次数。默认值是1000。

tolerance 一个浮点数，表示迭代中止的边界差值。默认值是0.0001。

positive 是布尔值，表示是否强制系数为正数。默认值是 false。

swColName 字符串，表示列名，必须为 X 中存在的列名。如果未指定该参数，则所有样本的权重都默认为1；如果指定该参数，则将指定的列作为自变量的权重。

checkInput 布尔值，表示是否检查输入参数（Y 和 X）的合法性。

  • 若 checkInput=true（默认值），则会检查参数中是否存在无效值（NULL），若存在，则会报错；

  • 若 checkInput=false，则不检查无效值。

注： 强烈建议开启 checkInput，以检查输入参数的有效性。如果不开启 checkInput，则必须确保输入参数中不存在无效值，并且中间计算过程中不会产生无效值，否则可能得到一个无用的模型。

例子

x1=1 3 5 7 11 16 23
x2=2 8 11 34 56 54 100
y=0.1 4.2 5.6 8.8 22.1 35.6 77.2;
print(lassoBasic(y, (x1,x2), mode = 0));
# output
[-9.133706333069543,2.535935196073186,0.189298948643987]


print(lassoBasic(y, (x1,x2), mode = 1));
# output
factor    beta               stdError          tstat              pvalue           
--------- ------------------ ----------------- ------------------ -----------------
intercept -9.133706333069543 5.247492365971091 -1.740584968222107 0.156730846105191
x1        2.535935196073186  1.835793667840723 1.38138356205138   0.239309472176311
x2        0.189298948643987  0.410201227095842 0.461478260277749  0.66843504931137 


print(lassoBasic(y, (x1,x2), mode = 2));
# output
Coefficient->
factor    beta               stdError          tstat              pvalue           
--------- ------------------ ----------------- ------------------ -----------------
intercept -9.133706333069543 5.247492365971091 -1.740584968222107 0.156730846105191
x1        2.535935196073186  1.835793667840723 1.38138356205138   0.239309472176311
x2        0.189298948643987  0.410201227095842 0.461478260277749  0.66843504931137 

RegressionStat->
item         statistics       
------------ -----------------
R2           0.931480447323074
AdjustedR2   0.897220670984611
StdError     8.195817208870076
Observations 7                

ANOVA->
Breakdown  DF SS                   MS                   F                  Significance     
---------- -- -------------------- -------------------- ------------------ -----------------
Regression 2  4165.242566095043912 2082.621283047521956 31.004574440904473 0.003672076469395
Residual   4  268.685678884843582  67.171419721210895                                       
Total      6  4471.637142857141952                                                          

Residual->
[6.319173239708383,4.21150915569809,-0.028258082380245,-6.254004293338318,-7.262321947798779,-6.063400030876729,9.077301958987561]