fminSLSQP

fminSLSQP(func, X0, [fprime], [constraints], [bounds], [ftol=1e-6], [epsilon], [maxIter=100])

func is the function to minimize. The return value of the function must be numeric type.

X0 is a numeric scalar or vector indicating the initial guess.

fprime (optional) is the gradient of func. If not provided, then func returns the function value and the gradient.

constraints (optional) is a vector of dictionaries. Each dictionary should include the following keys:

• type: A string indicating the constraint type, which can be 'eq' for equality constraints and 'ineq' for inequality constraints.
• fun: The constraint function. The return value must be a numeric scalar or vector.
• jac: The gradient function of constraint fun. The return value must be a numeric vector or a matrix. If the size of the return value of fun is m, and the size of the parameters to be optimized is n, then the shape of the return value of jac must be (n,m).

Note: The number of equality constraints in constraints cannot exceed the size of the parameters to be optimized. Let n be the number of parameters, k be the number of equality constraint functions, and len_i be the size of the return value of the i-th equality constraint function. The following condition must be satisfied: .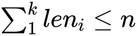

bounds (optional) is a numeric matrix indicating the bounds on parameters of X0. The matrix must be in the shape of (N,2), where N=size(X0). The two elements of each row defines the bounds (min, max) on that parameter. float("inf") can be specified for no bound in that direction.

ftol (optional) is a positive number indicating the precision requirement for the function value when the optimization stops. The default value is 1e-6.

epsilon (optional) is a positive number indicating the step size used for numerically calculating the gradient. The default value is 1.4901161193847656e-08.

maxIter (optional) is a non-negative integer indicating the maximum number of iterations. The default value is 15000.

Minimize a function using Sequential Least Squares Programming.

Return value: A dictionary with the following keys:

• xopt: A floating-point vector indicating the parameters of the minimum.
• fopt: A floating-point scalar indicating the value of func at the minimum, i.e., fopt=func(xopt).
• iterations: Number of iterations.
• mode: An integer indicating the optimization state. mode=0 means optimization succeeded, while other values indicate abnormal algorithm termination. For more information, refer to jacobwilliams - slsqp.

Minimize function rosen using Sequential Least Squares Programming:

def rosen(x) { 
	N = size(x);
	return sum(100.0*power(x[1:N]-power(x[0:(N-1)], 2.0), 2.0)+power(1-x[0:(N-1)], 2.0));
}

def rosen_der(x) {
	N = size(x);
	xm = x[1:(N-1)]
	xm_m1 = x[0:(N-2)]
	xm_p1 = x[2:N]
	der = array(double, N)
	der[1:(N-1)] = (200 * (xm - xm_m1*xm_m1) - 400 * (xm_p1 - xm*xm) * xm - 2 * (1 - xm))
	der[0] = -400 * x[0] * (x[1] - x[0]*x[0]) - 2 * (1 - x[0])
	der[N-1] = 200 * (x[N-1] - x[N-2]*x[N-2])
	return der
}

def eq_fun(x) {
	return 2*x[0] + x[1] - 1
}

def eq_jac(x) {
	return [2.0, 1.0]
}

def ieq_fun(x) {
	return [1 - x[0] - 2*x[1], 1 - x[0]*x[0] - x[1], 1 - x[0]*x[0] + x[1]]
}

def ieq_jac(x) {
	ret = matrix(DOUBLE, 2, 3)
	ret[0,:] = [-1.0, -2*x[0], -2*x[0]]
	ret[1,:] = [-2.0, -1.0, 1.0]
	return ret
}

eqCons=dict(STRING, ANY)
eqCons[`type]=`eq
eqCons[`fun]=eq_fun
eqCons[`jac]=eq_jac

ineqCons=dict(STRING, ANY)
ineqCons[`type]=`ineq
ineqCons[`fun]=ieq_fun
ineqCons[`jac]=ieq_jac

cons = [eqCons, ineqCons]

X0 = [0.5, 0]
bounds = matrix([0 -0.5, 1.0 2.0])
res = fminSLSQP(rosen, X0, rosen_der, cons, bounds, 1e-9)
res;

Output:

mode->0
xopt->[0.414944749170,0.170110501659]
fopt->0.342717574994
iterations->4