mpercentileTopN
Syntax
mpercentileTopN(X, S, percent, window, top, [interpolation],
[ascending])
Please see mTopN for the parameters and windowing logic.
Arguments
X is a numeric vector, matrix or table.
S is a numeric/temporal vector, matrix or table, based on which X are sorted.
percent is an integer or floating value between 0 and 100.
interpolation (optional) is a string indicating the interpolation method to use if the specified percentile is between two elements in X (assuming the ith and (i+1)th element in the sorted X) . It can take the following values:
-
'linear' (default): Return Xi + (Xi+1 - Xi)* fraction, where
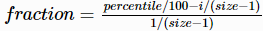
-
'lower': Return Xi
-
'higher': Return Xi+1
-
'nearest': Return Xi+1 or Xi that is closest to the specified percentile
-
'midpoint': Return (Xi+1 + Xi)/2
Details
-
When X is a vector, within a sliding window of given length (measured by the number of elements), the function stably sorts X by S in the order specified by ascending, then calculates the moving percentile rank of the first top elements.
-
When X is a matrix or table, conduct the aforementioned calculation within each column of X. The result is a matrix/table with the same shape as X.
Examples
When X is a vector:
x = [2,,8,0,4,,6,3,5,7]
s = [,1,8,7,9,6,5,0,4,3]
mpercentileTopN(x, s, percent=25, window=6, top=3, interpolation="lower")
// output: [,,8,0,0,0,6,3,3,3]
mpercentileTopN(x, s, percent=75, window=6, top=3, interpolation="higher")
// output: [,,8,8,8,0,6,6,6,7]
mpercentileTopN(x, s, percent=5, window=6, top=3, interpolation="nearest")
// output: [,,8,0,0,0,6,3,3,3]
mpercentileTopN(x, s, percent=15, window=6, top=3, interpolation="midpoint")
// output: [,,8,4,4,0,6,4.5,4,4]
mpercentileTopN(x, s, percent=50, window=6, top=3, interpolation="linear")
// output: [,,8,4,4,0,6,4.5,5,5]When X is a matrix:
x = [8,,1,6,9,2,0,,5,3,2,,8,0,4,,6,3,5,7]$10:2
s = [,1,8,7,9,6,5,0,4,3]
mpercentileTopN(x, s, percent=15, window=6, top=3, interpolation="midpoint")Output:
| #0 | #1 |
|---|---|
| 1 | 8 |
| 3.5 | 4 |
| 3.5 | 4 |
| 4 | 0 |
| 1 | 6 |
| 1 | 4.5 |
| 2.5 | 4 |
| 4 | 4 |
