计算精度问题与 DECIMAL 类型
1. DECIMAL 的计算特性
1.1. DECIMAL 的计算方式
DECIMAL 的存储分为两部分,即存储整型数据的 raw data 和存储小数位数的 scale。例如,对于DECIMAL32(2) 类型的 1.23, 它存储了两个数据:(1) raw data:即整型 123,(2) scale:即 2。这样存储的好处是,在计算时可以直接使用整型的 raw data 进行计算,从而避免精度损失。
对于大多数计算函数,如果最后返回的结果是浮点数类型,DECIMAL 在进行计算时, 会使用 raw data 参与计算,尽量延迟转换成浮点数的时机,从而确保得到精确结果。比如计算 avg 时,假设数据为 DECIMAL32(2) 类型:[1.11, 2.22, 3.33],其 raw data 为:[111, 222, 333]。在计算时,先算出 raw data 的 sum:111 + 222 + 333 = 666,然后转换成浮点数:double(666) / 102 / 3 = 2.22。
对于DECIMAL算术运算的规则,可参照:DECIMAL.md。
1.2. DECIMAL 的计算输出
本节主要讲述DECIMAL作为计算函数输入的输出结果。
在 DolphinDB 计算函数中,以 DECIMAL 类型作为输入,输出结果仍为 DECIMAL 类型的函数较少,仅有:sum、max、min、first、last、firstNot、lastNot 及其 cum、m、tm、TopN 系列函数,如 cummax、mmin、tmsum、msumTopN,cumsumTopN,tmsumTopN 等;以及 cumPositiveStreak。
a = decimal64(rand(10,100),4)
typestr(sum(a))
>> DECIMAL128
typestr(cummax(a))
>> FAST DECIMAL64 VECTOR
typestr(mmin(a,5))
>> FAST DECIMAL64 VECTOR
T = 2023.03.23..2023.06.30
typestr(tmsum(T, a, 3))
>> FAST DECIMAL128 VECTOR
typestr(cumPositiveStreak(a))
>> FAST DECIMAL128 VECTOR需要注意的是,在引入 DECIMAL128 类型后,自 2.00.10 版本起,sum 系列函数和 cumPositiveStreak 的输入输出类型对应规则如下:
| 计算函数 | 输入类型 | 输出类型 |
|---|---|---|
| sum/cumsum/msum/tmsum/msumTopN/cumsumTopN/tmsumTopN/cumPositiveStreak | DECIMAL32 | DECIMAL64 |
| DECIMAL64 | DECIMAL128 | |
| DECIMAL128 | DECIMAL128 |
除了上述函数外,cum、m、tm、TopN 系列的函数,包括它们对应的原始的函数,比如 avg、std、var、skew 等,以 DECIMAL 类型作为输入,都将返回 DOUBLE 类型的输出结果。
a = decimal64(rand(10,100),4)
typestr(avg(a))
>> DOUBLE
typestr(cumstd(a))
>> FAST DOUBLE VECTOR
typestr(mvar(a,5))
>> FAST DOUBLE VECTOR
T = 2023.03.23..2023.06.30
typestr(tmskew(T, a, 3))
>> FAST DOUBLE VECTOR下面将以 DECIMAL64 作为输入为例,列出常见计算函数的输出结果类型。
| 计算函数 | 输入类型 | 输出类型 |
|---|---|---|
| sum/cumsum/msum/tmsum | DECIMAL64 | DECIMAL128 |
| msumTopN/cumsumTopN/tmsumTopN | DECIMAL64 | DECIMAL128 |
| max/cummax/mmax/tmmax | DECIMAL64 | DECIMAL64 |
| min/cummin/mmin/tmmin | DECIMAL64 | DECIMAL64 |
| first/mfirst/tmfirst | DECIMAL64 | DECIMAL64 |
| last/mlast/tmlast | DECIMAL64 | DECIMAL64 |
| firstNot/cumfirstNot | DECIMAL64 | DECIMAL64 |
| lastNot/cumlastNot | DECIMAL64 | DECIMAL64 |
| cumPositiveStreak | DECIMAL64 | DECIMAL128 |
| avg/cumavg/mavg/tmavg/mavgTopN/cumavgTopN/tmavgTopN | DECIMAL64 | DOUBLE |
| sum2/cumsum2/msum2/tmsum2 | DECIMAL64 | DOUBLE |
| prod/cumprod/mprod/tmprod | DECIMAL64 | DOUBLE |
| med/cummed/mmed/tmmed | DECIMAL64 | DOUBLE |
| std/cumstd/mstd/tmstd/mstdTopN/cumstdTopN/tmstdTopN | DECIMAL64 | DOUBLE |
| skew/mskew/tmskew/mskewTopN/cumskewTopN/tmskewTopN | DECIMAL64 | DOUBLE |
| kurtosis/mkurtosis/tmkurtosis/mkurtosisTopN/cumkurtosisTopN/tmkurtosisTopN | DECIMAL64 | DOUBLE |
| corr/cumcorr/mcorr/tmcorr/mcorrTopN/cumcorrTopN/tmcorrTopN | DECIMAL64 | DOUBLE |
| covar/cumcovar/mcovar/tmcovar/mcovarTopN/cumcovarTopN/tmcovarTopN | DECIMAL64 | DOUBLE |
| beta/cumbeta/mbeta/tmbeta/mbetaTopN/cumbetaTopN/tmbetaTopN | DECIMAL64 | DOUBLE |
2. DECIMAL 的优缺点
2.1. DECIMAL 的优点
实数在计算机内部无法被精确地表示为浮点数的原因主要有两个:第一个原因是类似于 0.1 这样的数字,具有有限的十进制表示,但是在二进制中能表示为无穷重复的数据,等于 0.1 的近似值,无法被精确表示;第二个原因是数值超出了数据类型能表示的数值范围,系统将对数据做一定处理。与浮点数相比,DECIMAL 类型最大的优点,就在于它能够精确地表示和计算数据。
例如,在表示123.0001时:
a =123.0001
print(a)
>> 123.000100000000003
b = decimal64(`123.0001,15)
print(b)
>> 123.000100000000000可见,浮点数无法精确表示123.0001,而 DECIMAL 可以。
在计算 avg 时:
a = array(DOUBLE,0)
for (i in 1..100){
a.append!(123.0000+0.0003*i)
}
avg(a)
>> 123.015149999999
avg(a) == 123.01515
>> false
eqFloat(avg(a),123.01515)
>> true
b= array(DECIMAL64(4),0)
for (i in 1..100){
b.append!(123.0000+0.0003*i)
}
avg(b)
>> 123.015150000000
typestr(avg(b))
>> DOUBLE
avg(b) == 123.01515
>> true可见,在进行 avg 计算时,浮点数没有返回精确结果,而 DECIMAL 虽然返回结果也是 DOUBLE 类型,但返回了精确结果。
2.2. DECIMAL 的缺点
2.2.1. 容易溢出
DECIMAL32/DECIMAL64/DECIMAL128 类型的数值范围如下表所示,其中,DECIMAL32(S)、DECIMAL64(S) 和 DECIMAL128(S) 中的 S 表示保留的小数位数。
| 底层存储数据类型 | 字节占用 | Scale有效范围 | 有效数值范围 | 最大表示位数 | |
|---|---|---|---|---|---|
| DECIMAL32 | int32_t | 占用4个字节 | [0,9] | (-1 * 10 (9 - S), 1 * 10 (9 - S)) | 9位 |
| DECIMAL64 | int64_t | 占用8个字节 | [0,18] | (-1 * 10 (18 - S), 1 * 10 (18 - S)) | 18位 |
| DECIMAL128 | int128_t | 占用16个字节 | [0,38] | (-1 * 10 (38 - S), 1 * 10 (38 - S)) | 38位 |
在有效数值范围和最大表示位数的限制下,DECIMAL 类型很容易溢出。自 2.00.10 版本起,我们支持算术运算溢出后,若存在更高精度的类型,则将自动拓展结果的数据类型,从而降低溢出风险:
version 2.00.9.6:
a = decimal32(4.0000,4)
b = decimal32(8.0000,4)
c = a*b
>> Server response: 'c = a * b => Decimal math overflow'
version 2.00.10:
a = decimal32(4.0000,4)
b = decimal32(8.0000,4)
c = a*b
print(c)
>> 32.00000000
typestr(c)
>> DECIMAL64但即使如此,DECIMAL128 仍存在溢出风险:
a = decimal128(36.00000000,8)
b = a*a*a*a
>> Server response: 'b = a * a * a * a => Decimal math overflow'如上所示,由于 DolphinDB 中 DECIMAL 类型的数据乘法运算结果的 scale 是逐个累加的,b 的预期结果将会是 1679616.00000000000000000000000000000000,将会有39位数字,超出了 DECIMAL128 的最大表示位数38位,导致了溢出。
2.00.10版本新增支持了 DECIMAL 类型的乘法函数 decimalMultiply,与 multiply 函数 (* 运算符) 相比,该函数可以指定计算结果的精度。当 DEICMAL 类型的乘法运算导致 scale 累加存在溢出风险时,可以按需使用 decimalMultiply 函数,指定计算结果精度。
a = decimal64(36.00000000,8)
decimalMultiply(a, a, 8)
>> 1296.000000002.2.2. 转换误差
当我们直接使用常量生成 DECIMAL 类型时,可能会因为浮点数的转换产生误差:
a = 0.5599
decimal64(a,4)
>> 0.5598为了避免这种误差,可以使用字符串来生成 DECIMAL:
a = "0.5599"
decimal64(a,4)
>> 0.55992.2.3. 内存占用
DECIMAL32、DECIMAL64 和 DECIMAL128 类型在内存中分别占用4个字节、8个字节和16个字节,而 FLOAT 和 DOUBLE 类型在内存中占用4个字节和8个字节。因此,在数据量相同的情况下,DECIMAL128 占用的内存是 DOUBLE 的两倍。
且由于算术运算溢出后,将自动拓展结果的数据类型,每次拓展后等量数据占用的内存将翻倍,存在一定的内存风险。
2.2.4. 性能差异
与 FLOAT 和 DOUBLE 类型相比,DECIMAL 类型的计算速度更慢,我们将在第三节中进行详细比较。
2.2.5. 局限性
在 DolphinDB 中,DECIMAL 类型与 FLOAT/DOUBLE 类型相比,目前所支持的功能和结构较少。
- 在函数支持方面,尚有少部分计算函数不支持 DECIMAL 类型。
- 计算结果方面,cum, tm, m, TopN 系列的函数,包括它们对应的原始的函数(
sum、max、min、firstNot、lastNot、cumPositiveStreak除外),即使原始数据是 DECIMAL 类型,返回结果还是浮点数类型。 - 数据结构方面,DolphinDB 系统目前暂未支持 DECIMAL 类型在 matrix 和 set 中使用。
- 数据类型转换方面,DolphinDB 系统暂不支持 BOOL/CHAR/SYMBOL/UUID/IPADDR/INT128 等类型和 temporal 集合下的时间相关类型与 DECIMAL 类型相互转换,其中 STRING/BLOB 类型的数据如需转换成 DECIMAL 类型,必须满足 STRING/BLOB 类型的数据可以转换成数值类型的前提。
3. 浮点数与 DECIMAL 计算性能差异比较
为了比较浮点数类型与 DECIMAL 类型的计算性能差异,我们选取了一些常用的计算函数,比较相同数据情况下,各个数据类型的计算耗时。
首先,模拟数据脚本如下:
n = 1000000
data1 = rand(float(100.0),n)
data2 = double(data1)
data3 = decimal32(data1,4)
data4 = decimal64(data1,4)
data5 = decimal128(data1,4)随后,使用 timer 语句统计常用计算函数对于各个类型数据的计算耗时:
timer(100){sum(data1)} //执行100次,避免单次计算误差,并放大不同类型间的耗时差异
timer(100){sum(data2)}
timer(100){sum(data3)}
timer(100){sum(data4)}
timer(100){sum(data5)}
... ...得到的计算耗时统计结果如下(单位:ms):
| FLOAT | DOUBLE | DECIMAL32 | DECIMAL64 | DECIMAL128 | |
|---|---|---|---|---|---|
| sum | 52.985 | 64.331 | 28.721 | 57.234 | 107.126 |
| sum2 | 173.278 | 211.772 | 176.261 | 180.051 | 603.422 |
| prod | 63.650 | 55.641 | 171.718 | 174.389 | 18850.009 |
| avg | 178.086 | 210.495 | 26.094 | 106.869 | 258.508 |
| std | 362.388 | 345.758 | 278.933 | 319.177 | 968.276 |
| kurtosis | 547.751 | 407.561 | 585.859 | 769.879 | 1013.591 |
| skew | 546.705 | 439.348 | 622.758 | 842.994 | 1074.128 |
根据上述统计结果,可以得知:
(1)对于大部分计算函数,DECIMAL 的性能都比 FLOAT/DOUBLE 差;
(2)DECIMAL128 在计算时,会转换成 LONG DOUBLE(DECIMAL32/DECIMAL64 会转换成 DOUBLE),而 LONG DOUBLE 的实现取决于编译器和 CPU,可能是 12 字节或者 16 字节,LONG DOUBLE 的乘法在数据很大时非常耗时。在本节的测试样例中,vector 里的元素的取值范围较大,所以其乘积非常大,计算非常耗时。而如果把取值范围取小一些,比如 [0.5, 1.0],则 DECIMAL128 的计算和 DECIMAL32/DECIMAL64 相差不大;
(3)对于 sum、avg、std 这样的函数,DECIMAL 类型在计算时都没有做循环展开,而浮点数类型对 sum 做了循环展开,avg 则没有。此外,由于 DECIMAL 计算时会使用 raw data 先参与计算,再直接返回 DECIMAL 类型或转化为浮点数,本质是整型计算,实际过程比浮点数运算更高效。因此,它们的性能相差不大,甚至 DECIMAL32/DECIMAL64 的性能比 FLOAT/DOUBLE 更好。
4. DECIMAL 最佳实践:避免 mavg 计算精度损失
本节将以具体场景,比较 DECIMAL 类型和浮点数类型在实际计算中的精度差异。
mavg 和 moving(avg,…) 虽然在含义上完全相同,但两者的实现方式并不一致。mavg 的算法是:随着窗口的移动,总和加上进入窗口的数,减去离开窗口的数,再计算 avg,所以在这个加减的过程中,会产生浮点数精度问题。
首先,我们导入样例数据 tick.csv,原始数据类型均为 DOUBLE 类型,并计算 mavg、moving(avg,…):
data = loadText("<yourDirectory>/tick.csv")
t = select
MDTime,
((LastPx - prev(LastPx)) / (prev(LastPx) + 1E-10) * 1000) as val,
mavg(((LastPx - prev(LastPx)) / (prev(LastPx) + 1E-10) * 1000), 20, 1),
moving(avg, ((LastPx - prev(LastPx)) / (prev(LastPx) + 1E-10) * 1000), 20, 1)
from data得到的结果如下图所示:
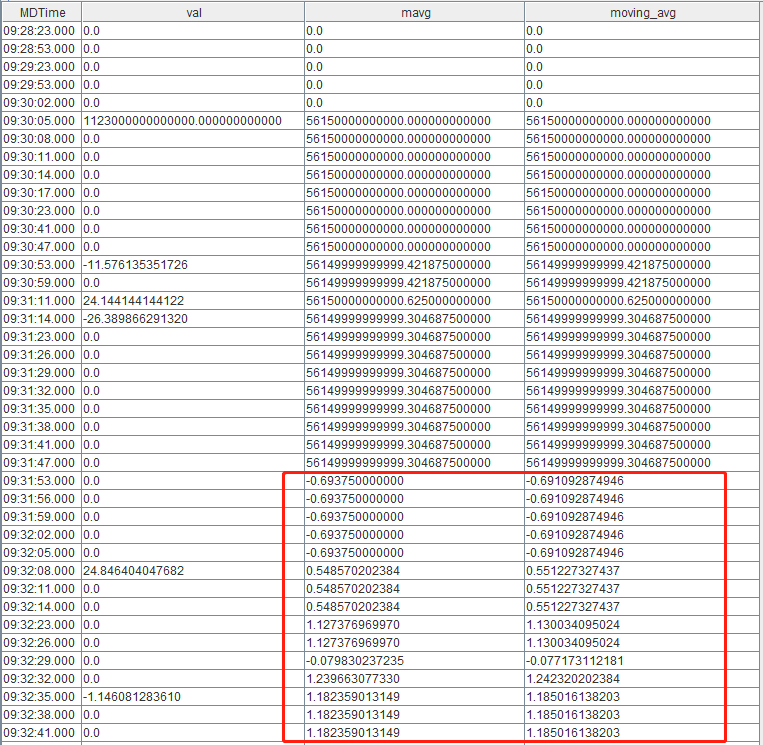
可以看到,计算结果从09:31:53.000开始产生误差。
为了避免这种计算误差,我们先将中间计算结果转换为 DECIMAL128 类型,再计算 mavg 和 moving(avg,…):
t = select
MDTime,
((LastPx - prev(LastPx)) / (prev(LastPx) + 1E-10) * 1000) as val,
mavg(decimal128(((LastPx - prev(LastPx)) / (prev(LastPx) + 1E-10) * 1000),12), 20, 1),
moving(avg, decimal128(((LastPx - prev(LastPx)) / (prev(LastPx) + 1E-10) * 1000),12), 20, 1)
from data得到的结果如下图所示:
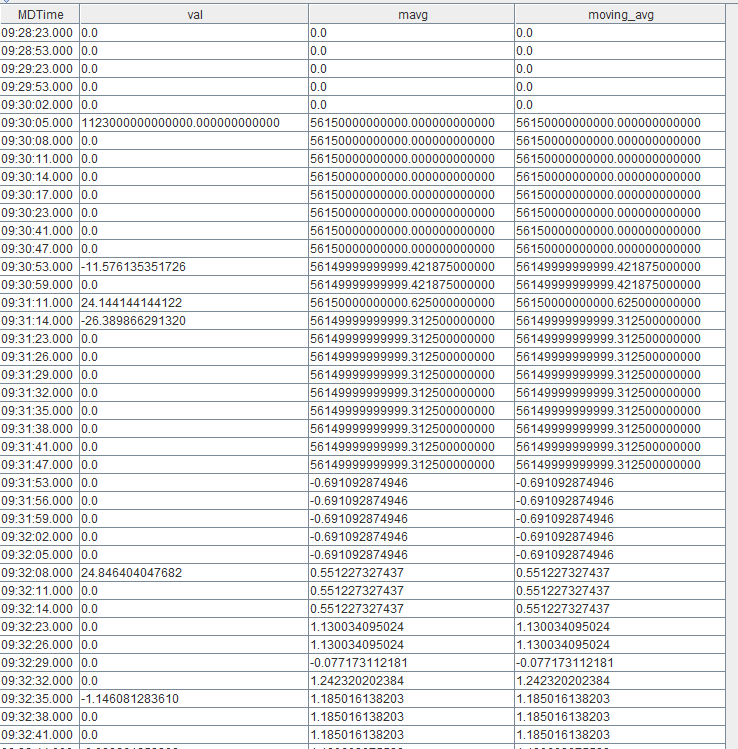
可以看到,mavg 和 moving(avg,…) 的计算结果完全一致。
由于浮点数的精度问题,cum, tm, m, TopN 系列的函数,包括它们对应的原始的函数,比如 avg、std 等,都有可能导致计算的精度误差。在对精度极为关注的场景下,我们推荐使用 DECIMAL 进行计算。需要注意的是,除了 sum、max、min、firstNot、lastNot、cumPositiveStreak 及其对应的系列函数,在入参是 DECIMAL 类型时能够返回 DECIMAL 类型的计算结果,其他函数都将返回浮点数类型。虽然存在一定的 DECIMAL 类型转换为浮点数类型的精度误差风险,但避免了计算过程中的精度损失,也可以对计算结果使用 round 函数或再次转换为 DECIMAL 类型,得到相对精确的结果。
5. 总结
浮点数由于其实现方式,在计算机内部无法精确地表示某些数值,因而容易出现精度误差,导致存储或计算结果与预期不符。DECIMAL 可以精确表示数值,但存在容易溢出、内存占用大、性能较劣、有一定局限性等缺点。尽管如此,在某些场景中,选用 DECIMAL 类型依旧能够很好地避免存储或计算结果与预期不符的情况出现。
综上所述,在实际应用时,需要考虑具体需要,选用合适的数据类型,对数据进行相应的精度管理。
