quadprog
Syntax
quadprog(H, f, [A], [b], [Aeq], [beq])
Parameters
H, A and Aeq must be matrices with the same number of columns.
f, b and beq are vectors.
A is the coefficient matrix of linear inequality constraints.
b is the right-hand-side vector of the linear inequality constraint.
Aeq is a linear equality constraint coefficient matrix.
beq is the right-hand-side vector of the linear equality constraint.
Details
Solve the following optimization problem with a quadratic objective function and a set of linear constraints.
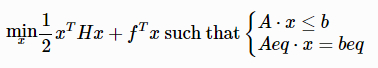
The result is a 2-element tuple. The first element is the minimum value of the objective function. The second element is the value of x where the value of the objective function is minimized.
Examples
Example 1: Find the minimum of 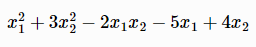
H=matrix([2 -2,-2 6])
f=[-5,4]
x=quadprog(H,f);
x[0];
// output: -6.375
x[1];
// output: [2.75,0.25]Example 2: Find the minimum of
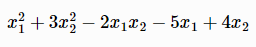
subject to the constraints of
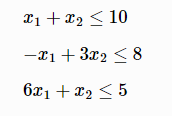
H=matrix([2 -2,-2 6])
f=[-5,4]
A=matrix([1 -1 6, 1 3 1])
b=[10, 8, 5]
x=quadprog(H,f,A,b);
x[0];
// output: -4.092975
x[1];
// output: [0.904959, -0.429752]Example 3: Find the minimum of
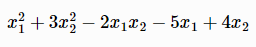
subject to the constraints of
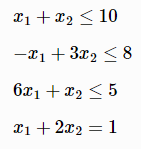
H=matrix([2 -2,-2 6])
f=[-5,4]
A=matrix([1 -1 6, 1 3 1])
b=[10, 8, 5]
Aeq=matrix([1],[2])
beq=[1]
x=quadprog(H,f,A,b,Aeq,beq);
x[0];
// output: -3.181818
x[1];
// output: [0.818182,0.090909]The 3 examples above share the same objective function. Example 1 has no constaints and achieves the lowest minimum value. Example 3 has more constaints than example 2 and therefore can only achieve a higher minimum value than both example 2 and example 1.
